Modern cosmology relies on the Freidman-Lemaitre-Robertson-Walker
(FLRW) metric. The FLRW metric is an exact solution of Einstein’s
field equations of general relativity under the assumption of a
simply connected, homogeneous, isotropic expanding or contracting
universe. The Freidman-Lemaitre-Robertson-Walker model serves as a
first approximation for the evolution of the universe, however
additional models have been added to provide for the deviation of the
observed universe from homogeneity and isotropy. In order to
understand the impact that the UG theory may have on cosmology, it is
essential to first understand to what extent the UG theory is
compatible with the general theory of relativity.
Section
VII-1: The General Theory of Relativity and Unified Gravitation
For most engineering and scientific applications, the quantitative
differences between Newton’s theory of gravitation and
Einstein’s relativistic theories are insignificant. Special
relativity and general relativity become important when velocities
within the system of interest approach the speed of light, or in
environments of high matter densities such as collapsed stars,
neutron stars or black holes, or for analyzing systems of
cosmological proportions.
Whereas Newton’s potential energy equation is given by
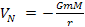 ,
the UG potential energy is described by ,
the UG potential energy is described by 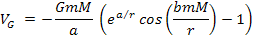
In contrast to Newtonian gravitation, the UG potential energy is a
non-linear function of the mass of the fundamental test particle.
Following equation 2-1-5, the acceleration of a non-relativistic test
particle of mass
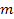 interacting with a particle of mass
interacting with a particle of mass
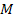 at rest at the origin of the frame of reference is given by
at rest at the origin of the frame of reference is given by
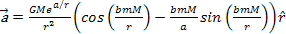 ,
instead of the Newtonian ,
instead of the Newtonian
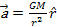 .
Therefore, within the potential energy oscillation zone at
distances of the order of .
Therefore, within the potential energy oscillation zone at
distances of the order of
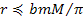 or
or
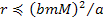 ,
the trajectory and acceleration of a free falling test particle
becomes dependent on its mass.1
However, at distances ,
the trajectory and acceleration of a free falling test particle
becomes dependent on its mass.1
However, at distances
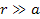 , ,
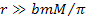 and
and
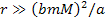 ,
the acceleration of the test particle approaches the Newtonian
acceleration of ,
the acceleration of the test particle approaches the Newtonian
acceleration of
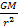 ,
and becomes virtually independent of its mass ,
and becomes virtually independent of its mass
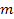 . .
As the special theory of relativity is restricted to systems with
relatively negligible gravitation, the deviation of the UG theory
from Newton’s theory of gravitation does not pose any
additional conflict that has not already been expressed by the
Newtonian theory. However, the general theory of relativity is based
on Einstein’s equivalence principle, stating that the
trajectory of a free falling test particle depends only on its
initial position and velocity, and is independent of its composition
(and therefore independent of its mass). Consequently, at short
distances such as
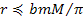 and
and
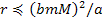 ,
the UG theory is possibly at odds with general relativity. ,
the UG theory is possibly at odds with general relativity.
Regardless of whether or not the UG theory is correct, the viability
of the principle of equivalence and general relativity at short
distances (under
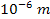 )
is arguable. In general relativity the applicability of the
equivalence principle is restricted to distance scales where the
gravitational field is uniform (with negligible tidal forces).
Therefore, the equivalence principle cannot be applied at short
distances, where the Newtonian forces may change drastically with any
small deviation in the distance )
is arguable. In general relativity the applicability of the
equivalence principle is restricted to distance scales where the
gravitational field is uniform (with negligible tidal forces).
Therefore, the equivalence principle cannot be applied at short
distances, where the Newtonian forces may change drastically with any
small deviation in the distance
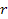 .
In addition, quantum effects become substantial at distances .
In addition, quantum effects become substantial at distances
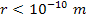 .
Despite decades of enormous effort, the consolidation of general
relativity with quantum mechanics has yet to succeed, raising further
doubt about the viability of the equivalence principle at extremely
short distances. Furthermore, according to the standard model, the
strong interaction and the weak interaction are highly dependent on
particle masses, and become dominant at distances of approximately .
Despite decades of enormous effort, the consolidation of general
relativity with quantum mechanics has yet to succeed, raising further
doubt about the viability of the equivalence principle at extremely
short distances. Furthermore, according to the standard model, the
strong interaction and the weak interaction are highly dependent on
particle masses, and become dominant at distances of approximately
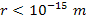 .
The exact equations of the strong and the weak forces within the
standard model are unknown, however they are not likely to be linear
with the mass of the test particle. Therefore, the equivalence
principle may not be applied on such small scales, regardless of the
validity of the UG theory. .
The exact equations of the strong and the weak forces within the
standard model are unknown, however they are not likely to be linear
with the mass of the test particle. Therefore, the equivalence
principle may not be applied on such small scales, regardless of the
validity of the UG theory.
It is important to determine when and where the UG equations
substantially deviate from general relativity. According to equation
2-1-5 of the UG theory, the acceleration rates of free falling
protons, neutrons and electrons are not identical when they
gravitationally interact with ordinary matter at distances less than
or of the order of
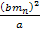 .
Therefore, in theory, within this range of distances, a free falling
frame is not necessarily an inertial frame, as different free falling
particles or objects within the same frame may demonstrate different
rates of acceleration. .
Therefore, in theory, within this range of distances, a free falling
frame is not necessarily an inertial frame, as different free falling
particles or objects within the same frame may demonstrate different
rates of acceleration.
However, at interaction distances of
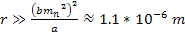 (where
(where
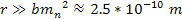 and
and
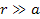 ,
thus ,
thus
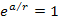 ),
the gravitational force applied on a free falling ordinary particle
is virtually Newtonian, and its acceleration is therefore independent
of its mass. Consequently, in a UG world composed entirely of
protons electrons and neutrons (as well as their anti-particles) the
general theory of relativity provides a good approximation at
distances of ),
the gravitational force applied on a free falling ordinary particle
is virtually Newtonian, and its acceleration is therefore independent
of its mass. Consequently, in a UG world composed entirely of
protons electrons and neutrons (as well as their anti-particles) the
general theory of relativity provides a good approximation at
distances of
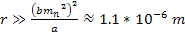 .
Consequently, in environments where ordinary matter interactions are
dominant and the influence of superheavy particles can be regarded as
negligible, the predictions made by general relativity, such as
gravitational redshift (or blueshift), gravitational time dilation,
the deflection of light by gravity (as in gravitational lensing) and
the relativistic precession of apsides, hold true and are compatible
with the UG theory. .
Consequently, in environments where ordinary matter interactions are
dominant and the influence of superheavy particles can be regarded as
negligible, the predictions made by general relativity, such as
gravitational redshift (or blueshift), gravitational time dilation,
the deflection of light by gravity (as in gravitational lensing) and
the relativistic precession of apsides, hold true and are compatible
with the UG theory.
According to the fourth UG postulate, however, massive superheavy
particles are produced in environments of extremely high matter
density, such as in the vicinity of collapsed stars, neutron stars or
non-singular black holes.2
When a test particle of mass
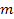 (or an object composed of particles of mass
(or an object composed of particles of mass
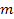 )
interacts with a massive SHP of mass )
interacts with a massive SHP of mass
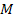 ,
the non-linear distance range of the UG force, where the cosine and
the sine terms of equation 2-1-5 demonstrate oscillations, increases
with the product of the two particles’ masses ,
the non-linear distance range of the UG force, where the cosine and
the sine terms of equation 2-1-5 demonstrate oscillations, increases
with the product of the two particles’ masses
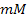 .
Therefore, if extremely large superheavy particles exist at the core
of a planet (where the term .
Therefore, if extremely large superheavy particles exist at the core
of a planet (where the term
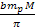 is of the order of tens or hundreds of thousands of kilometers) or
at the core of a galaxy (where
is of the order of tens or hundreds of thousands of kilometers) or
at the core of a galaxy (where
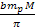 is of the order of tens of kiloparsecs),3
the gravitational oscillations create minimum points, arcs or
contours. For the case of
is of the order of tens of kiloparsecs),3
the gravitational oscillations create minimum points, arcs or
contours. For the case of
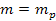 ,
ordinary matter (such as the molecules or atoms of an object orbiting
a planet, or of galactic interstellar gas) accumulates at the minima,
and may create rings or spirals. As the UG oscillations are
non-linear functions of the mass of the fundamental test particles,
the isolated electrons, protons or superheavy particles may
demonstrate substantially different rates of gravitational
acceleration on large distance scales. Consequently, a free falling
frame, and the free falling objects or particles within the frame,
may not accelerate at the same rate, and cannot be assumed to follow
the geodesics of curved spacetime geometry. Therefore, in regions of
spacetime where rings and spirals are formed, the UG theory
demonstrates greater deviation from the predictions of the general
theory of relativity. Discrepancies between the results of the UG
theory and general relativity, however, are relatively small in
subsystems influenced by external SHPs when the subsystems are too
mild to generate or sustain SHPs of their own, and their ordinary
matter is almost exclusively arranged in the form of neutral atoms,
molecules or more complex objects. In such a case, where all of the
matter within a local free falling frame is composed exclusively of
atoms and molecules of ordinary matter that interact with a strong
external SHP, each atom or molecule accelerates as a rigid object.
Therefore, all of the free falling objects within the local frame
accelerate at the same rate as the frame itself (note that the mass
of a neutron is almost equal to the mass of a proton, and the mass of
the electrons bonded to the nucleus of the atom is almost negligible
relative to the masses of the nucleons. The effect of the bonded
electrons on the object’s acceleration can therefore be
neglected, and the effect of a neutron on the overall acceleration of
the object is nearly identical to that of a proton.4
Consequently, the acceleration of the free falling objects is very
close to the acceleration rate of a free proton). Therefore, the
equivalence principle is valid as long as the frame is sufficiently
small to ensure that no significant tidal forces exist within its
limits, and as long as the number of free electrons or positrons
within the frame is negligible. When a significant number of free
electrons or positrons exist within the local frame, their rate of
acceleration according to the UG theory may vary from the
acceleration of the protons, atoms and molecules within the frame,5
as well as from the acceleration of the free falling frame.6
Consequently, the equivalence principle is violated, and the frame
does not constitute an inertial frame. The same is true for cases
where a significant portion of the free falling objects within the
given local frame are composed of massive SHP types as well. ,
ordinary matter (such as the molecules or atoms of an object orbiting
a planet, or of galactic interstellar gas) accumulates at the minima,
and may create rings or spirals. As the UG oscillations are
non-linear functions of the mass of the fundamental test particles,
the isolated electrons, protons or superheavy particles may
demonstrate substantially different rates of gravitational
acceleration on large distance scales. Consequently, a free falling
frame, and the free falling objects or particles within the frame,
may not accelerate at the same rate, and cannot be assumed to follow
the geodesics of curved spacetime geometry. Therefore, in regions of
spacetime where rings and spirals are formed, the UG theory
demonstrates greater deviation from the predictions of the general
theory of relativity. Discrepancies between the results of the UG
theory and general relativity, however, are relatively small in
subsystems influenced by external SHPs when the subsystems are too
mild to generate or sustain SHPs of their own, and their ordinary
matter is almost exclusively arranged in the form of neutral atoms,
molecules or more complex objects. In such a case, where all of the
matter within a local free falling frame is composed exclusively of
atoms and molecules of ordinary matter that interact with a strong
external SHP, each atom or molecule accelerates as a rigid object.
Therefore, all of the free falling objects within the local frame
accelerate at the same rate as the frame itself (note that the mass
of a neutron is almost equal to the mass of a proton, and the mass of
the electrons bonded to the nucleus of the atom is almost negligible
relative to the masses of the nucleons. The effect of the bonded
electrons on the object’s acceleration can therefore be
neglected, and the effect of a neutron on the overall acceleration of
the object is nearly identical to that of a proton.4
Consequently, the acceleration of the free falling objects is very
close to the acceleration rate of a free proton). Therefore, the
equivalence principle is valid as long as the frame is sufficiently
small to ensure that no significant tidal forces exist within its
limits, and as long as the number of free electrons or positrons
within the frame is negligible. When a significant number of free
electrons or positrons exist within the local frame, their rate of
acceleration according to the UG theory may vary from the
acceleration of the protons, atoms and molecules within the frame,5
as well as from the acceleration of the free falling frame.6
Consequently, the equivalence principle is violated, and the frame
does not constitute an inertial frame. The same is true for cases
where a significant portion of the free falling objects within the
given local frame are composed of massive SHP types as well.
Section VII-2:
Unified Gravitation and Black Holes
In
the previous section it was demonstrated that in a world composed
exclusively of ordinary matter, the UG theory would not demonstrate
significant deviation from general relativity at distances greater
than
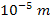 .
In such a scenario, the concept of a black hole event horizon, where
neither a particle nor light can escape once trapped below the
horizon, is supported by the UG theory.7
It is important to note, however, that the UG theory rules out the
concept of a black hole as a singularity. The fact that the UG
potential energy equation oscillates between sets of maxima and
minima, with a potential energy that approaches positive and negative
infinities as .
In such a scenario, the concept of a black hole event horizon, where
neither a particle nor light can escape once trapped below the
horizon, is supported by the UG theory.7
It is important to note, however, that the UG theory rules out the
concept of a black hole as a singularity. The fact that the UG
potential energy equation oscillates between sets of maxima and
minima, with a potential energy that approaches positive and negative
infinities as
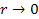 ,
requires an infinite amount of energy to physically combine two
massive particles. Therefore, matter cannot collapse into
singularity. Furthermore, in a universe containing a significant
amount of superheavy particles, the UG theory provides a mechanism by
which matter trapped within the event horizon of a black hole can
eventually escape. As the matter within a black hole collapses
toward its center, the pressure and temperature at the core become
extremely high, to the point where sufficiently large superheavy
particles may be created, generating their own repulsive zones. In
cases where the SHP mass becomes sufficiently large, the oscillation
range between the newly generated superheavy particles and ordinary
matter matches or exceeds the radius of the black hole event horizon
prior to the SHP creation. With a sufficiently high quantity of
superheavy particles, the repulsive force between SHPs and ordinary
matter may overcome the strong attractive forces exerted by the black
hole’s ordinary matter on matter located close to the former
event horizon, making it possible for matter to escape. ,
requires an infinite amount of energy to physically combine two
massive particles. Therefore, matter cannot collapse into
singularity. Furthermore, in a universe containing a significant
amount of superheavy particles, the UG theory provides a mechanism by
which matter trapped within the event horizon of a black hole can
eventually escape. As the matter within a black hole collapses
toward its center, the pressure and temperature at the core become
extremely high, to the point where sufficiently large superheavy
particles may be created, generating their own repulsive zones. In
cases where the SHP mass becomes sufficiently large, the oscillation
range between the newly generated superheavy particles and ordinary
matter matches or exceeds the radius of the black hole event horizon
prior to the SHP creation. With a sufficiently high quantity of
superheavy particles, the repulsive force between SHPs and ordinary
matter may overcome the strong attractive forces exerted by the black
hole’s ordinary matter on matter located close to the former
event horizon, making it possible for matter to escape.
Section VII-3:
The Effect of Unified Gravitation on Cosmology - The Big Bang
and the Expansion of the Universe
Hubble’s
discovery that the universe is not static, but expanding, led to the
development of the Big Bang cosmological model, which attributes the
beginning of our universe to an explosion from a very dense point
singularity at about 14.5 billion years ago. The recent discovery
that the universe is expanding at an accelerated rate forced the
reintroduction of the cosmological constant, which was initially
introduced into general relativity by Einstein in order to maintain a
static universe, and later retracted in response to Hubble’s
discovery of the expansion of the universe. Throughout its
development, the Big Bang model encountered significant problems, a
few of which were addressed in the introductory chapter of this book.
An entirely different approach may be taken via the UG theory. The
UG interaction between two particles has been demonstrated to produce
zones of attraction and zones of repulsion. The UG repulsive force
will be shown to account for the creation of large voids and to
explain the strong rejection between galactic entities,8
which drives galaxies to recede away from each other on large
distance scales and leads to the observed continuous, even
accelerated expansion of the universe. The interplay between
repulsive and attractive zones will be shown to account for the
creation of galaxies, as well as for the creation of galactic
groups, clusters and superclusters. Expansion due to repulsive
forces, rather than due to an expansion of spacetime and subsequent
inflation, may provide for a substantially simpler cosmological
model, which avoids the paradoxes and inconsistencies inherent in the
current Big Bang theory.
Section
VII-4: Galactic Lock Out
As a first step, the UG theory will be shown to predict that
sufficiently large and abundant superheavy particles within a galaxy
may create a gravitational barrier that rejects, and therefore
prevents most of the external ordinary matter from penetrating the
galactic disk.9
In other words, the galaxy will become “locked,” and its
growth halted. Consider, for example, an ordinary drifting object
(or test particle) approaching a galaxy from infinity with a
potential plus kinetic energy of close to zero.10
Initially, the object is located far beyond the maximal zonal range
of the galactic SHPs and is thus gravitationally attracted by the
galaxy’s ordinary matter.11
As it accelerates towards the galaxy, however, the object may reach a
distance where it is simultaneously attracted by the galaxy’s
ordinary matter and conversely repelled by the galactic superheavy
particles. Following equation 4-1-1, the object’s potential
energy is given by Equation
7-1 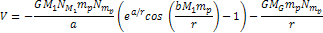
and
the force applied on the object is given by Equation
7-2 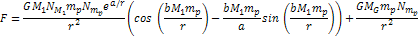
Note
that in order to concentrate on the essential factors, the above
equations are based on a hypothetical scenario of a simple galaxy
containing a single SHP group (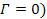 orbiting the center of the galaxy in a circular orbit of radius
orbiting the center of the galaxy in a circular orbit of radius
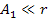 at a non-relativistic and constant velocity (therefore,
at a non-relativistic and constant velocity (therefore,
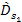 of equation 4-1-1 is equal to
of equation 4-1-1 is equal to
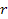 , ,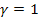 ,
and equation 4-1-1a converges toward equation 7-1). The vast portion
of the galaxy’s ordinary matter is assumed to be distributed
symmetrically around the center of the galaxy within a sphere of
radius ,
and equation 4-1-1a converges toward equation 7-1). The vast portion
of the galaxy’s ordinary matter is assumed to be distributed
symmetrically around the center of the galaxy within a sphere of
radius
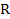 ,
where ,
where
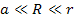 .
To further simplify the current discussion, the influence of other
external bodies is assumed to be negligible, and the effect of the
rotation of both the galaxy and its SHP groups on the overall energy
of the orbiting object is assumed to be relatively small. .
To further simplify the current discussion, the influence of other
external bodies is assumed to be negligible, and the effect of the
rotation of both the galaxy and its SHP groups on the overall energy
of the orbiting object is assumed to be relatively small.
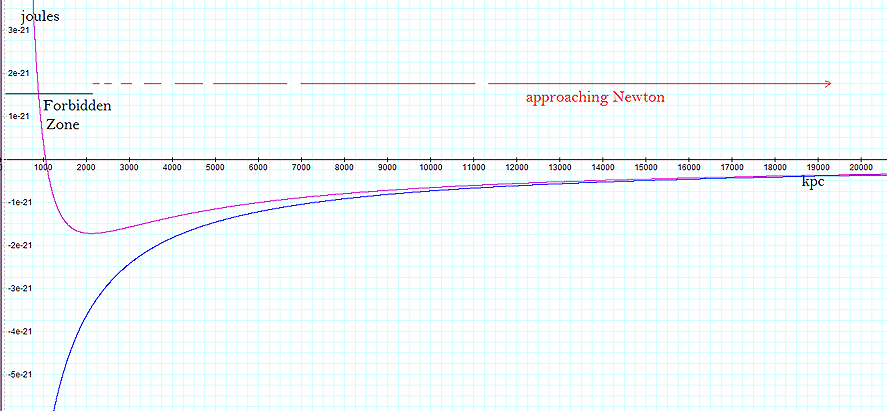
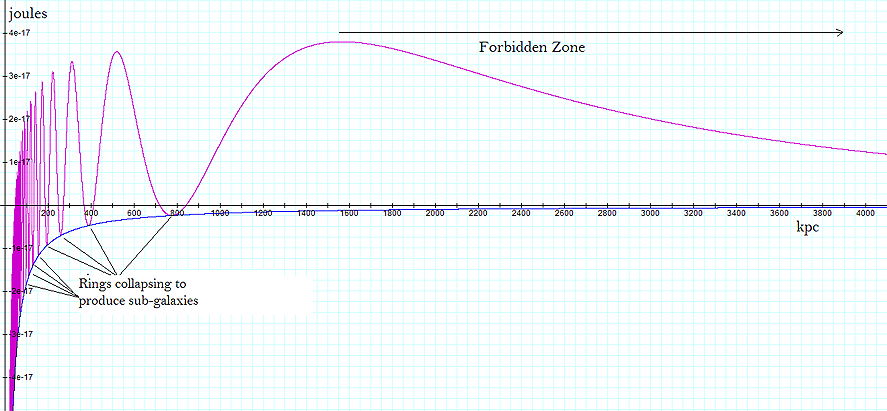
Figures 7-1a and 7-1b display the overall potential energy (via
equation 7-1) of an approaching single-particle object of mass
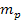 ,
as a function of its distance from the center of a galaxy containing
a single SHP of mass ,
as a function of its distance from the center of a galaxy containing
a single SHP of mass
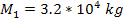 ,
and ordinary matter of a total mass of ,
and ordinary matter of a total mass of
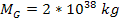 .12
The overall gravitational potential energy of the approaching
particle due to contributions of the SHP and ordinary matter is
indicated in violet. For comparison, the exclusive contribution of
the galaxy’s ordinary matter is displayed in blue. Note that
in this example, a drifting particle of zero energy cannot come
closer than a distance of about .12
The overall gravitational potential energy of the approaching
particle due to contributions of the SHP and ordinary matter is
indicated in violet. For comparison, the exclusive contribution of
the galaxy’s ordinary matter is displayed in blue. Note that
in this example, a drifting particle of zero energy cannot come
closer than a distance of about
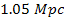 from the center of the galaxy (see figure 7-1b). Consequently, the
galaxy essentially becomes locked to an inflow of ordinary matter,
forbidding the entrance of any external ordinary particle of mass
from the center of the galaxy (see figure 7-1b). Consequently, the
galaxy essentially becomes locked to an inflow of ordinary matter,
forbidding the entrance of any external ordinary particle of mass
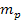 approaching with a potential plus kinetic energy below the
approaching with a potential plus kinetic energy below the
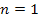 maximum of
maximum of
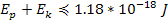 .
In addition, no circular orbit can exist between .
In addition, no circular orbit can exist between
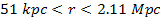 ,
as within this range of distance both the overall gravitational
force and the centrifugal force acting on the particle point outward,
and thus cannot cancel each other out.13 ,
as within this range of distance both the overall gravitational
force and the centrifugal force acting on the particle point outward,
and thus cannot cancel each other out.13
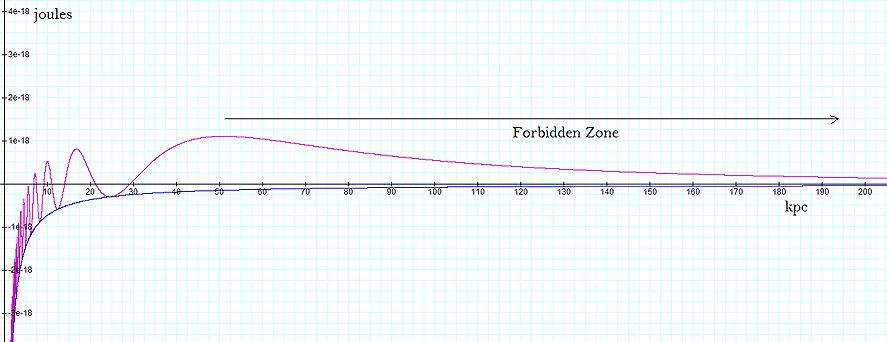
Figure
7-1a: The blue curve
in this figure displays the overall potential energy (derived via
equation 7-1) of an approaching single-particle object of mass 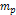 as a function of its distance from the center of a galaxy containing
a spherically symmetric distribution of ordinary matter of a total
mass of
as a function of its distance from the center of a galaxy containing
a spherically symmetric distribution of ordinary matter of a total
mass of 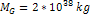 .
The addition of a single non-relativistic SHPof mass .
The addition of a single non-relativistic SHPof mass 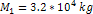 near the center of the galaxy is shown to elevate the potential
energy of the approaching particle (indicated in violet) and creates
a barrier at
near the center of the galaxy is shown to elevate the potential
energy of the approaching particle (indicated in violet) and creates
a barrier at 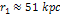 of
of 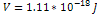 that keeps out all approaching particles of mass
that keeps out all approaching particles of mass 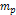 with an overall potential plus kinetic energy of less than
with an overall potential plus kinetic energy of less than 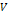 .
Within the resultant forbidden zone starting at .
Within the resultant forbidden zone starting at 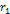 ,
a particle of mass ,
a particle of mass 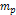 cannot be confined in orbit. The minima below
cannot be confined in orbit. The minima below 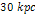 provide the locations of galactic rings,
where the collapse of these rings results in the production of
stars.
provide the locations of galactic rings,
where the collapse of these rings results in the production of
stars.
Figure
7-1b:The
potential energy is displayed over a distance range 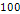 times greater. An external particle of mass
times greater. An external particle of mass 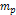 with an overall energy of
with an overall energy of 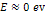 would be stopped by the SHP-generated
barrier at about
would be stopped by the SHP-generated
barrier at about 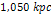 (or
(or 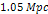 ).
The forbidden zone is demonstrated to extend all the way out to ).
The forbidden zone is demonstrated to extend all the way out to 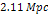 .
As the distance between the approaching particle and the center of
the galaxy increases beyond .
As the distance between the approaching particle and the center of
the galaxy increases beyond 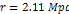 ,
the relative contribution of the SHP
to the potential energy of the test object declines, and the
particle’s potential energy converges toward the Newtonian
curve (in blue). ,
the relative contribution of the SHP
to the potential energy of the test object declines, and the
particle’s potential energy converges toward the Newtonian
curve (in blue).

Figure
7-1c: Provides the
force associated with the potential energy of the approaching
particle using the same parameters as figures 7-1a, 7-1b and equation
7-2. Note the repulsive force above 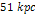 . .
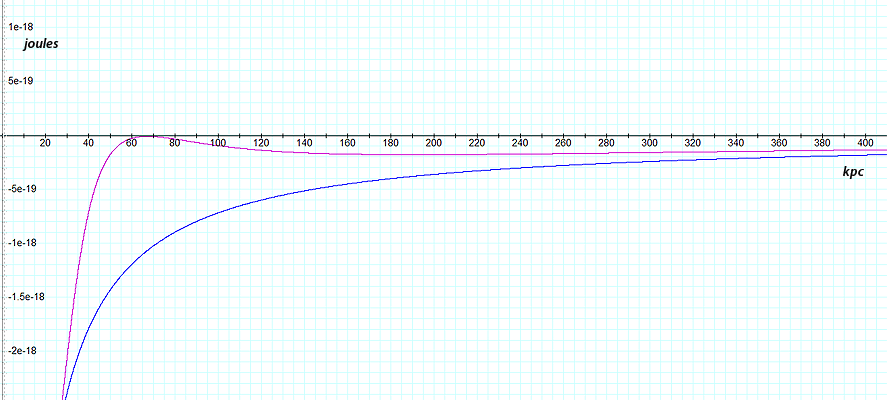
Figure 7-1d:The
height of the barrier reduces as the total mass of the galaxy’s
ordinary matter (within the barrier boundaries) increases and/or as
the number and mass of the dominant superheavy particles
are reduced. A drifting particle of mass 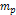 with a potential plus kinetic energy of about zero electron
volts is nearly prevented from entering the galaxy disk when the
maximum potential energy is at
with a potential plus kinetic energy of about zero electron
volts is nearly prevented from entering the galaxy disk when the
maximum potential energy is at 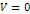 .
Such a case is demonstrated in this figure for a galaxy of overall
ordinary mass (within the barrier boundaries ) of .
Such a case is demonstrated in this figure for a galaxy of overall
ordinary mass (within the barrier boundaries ) of 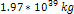 and when a single SHP of mass
and when a single SHP of mass 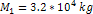 is located in the vicinity of the galactic center.
is located in the vicinity of the galactic center.
In general, the galaxy will
begin to lock out ordinary matter when 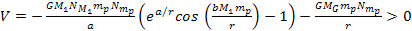 ,
or, as ,
or, as
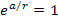 ,
when ,
when 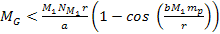 . .
Substituting
the approximate location of the maximum contour of the barrier at
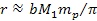 will provide
will provide
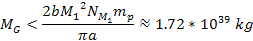
where
the parameter values used were
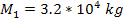 and
and
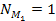 .
A detailed graphical analysis is displayed in figure 7-1d, providing
the mass .
A detailed graphical analysis is displayed in figure 7-1d, providing
the mass
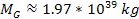 as the galaxy’s maximum amount of ordinary mass with which the
galaxy is still locked to drifting objects composed of ordinary
matter.
as the galaxy’s maximum amount of ordinary mass with which the
galaxy is still locked to drifting objects composed of ordinary
matter.
Section VII-5: The
Construction of a Barrier, the Effect of a Barrier on the
Fragmentation of a Collapsing Cloud and the Creation of a
Series of Distinct Galactic Entities
According to current theory, the stages of star formation and the
final state of a star are thought to depend on its overall mass. A
star of a mass greater than eight solar masses must pass through
successive stages of hydrogen, helium, carbon, neon, oxygen, and
silicon fusion at its center. With the passing of each stage, the
stellar core becomes increasingly hot and dense. The evolution of
stars is regarded as a long sequence of contractions, starting with
the initial collapse of a molecular cloud, which is then halted by
hydrogen burning, and ending with the formation of a neutron star or
black hole. The contraction process pauses several times, as nuclear
fusion provides the energy required to replenish the energy lost to
radiation and neutrinos, as well as the outward pressure needed to
balance the inward pull of the gravitational force. Upon the
exhaustion of one type of fuel, the star contracts, heats up and
burns the next higher element, usually created at a previous stage.
Eventually, a core of iron-group elements is produced. Since no
further energy-per-nucleon generating process is available, nuclear
fusion is halted and the star is held by the pressure created by
electron degeneration. As the amount of energy loss increases, the
electrons combine into the iron-group nuclei, raising their neutron
number. The energy of the stellar core again reduces to a level
where it can no longer balance the inward gravitational forces, and
the iron core collapses (at a rate of about a quarter of the speed of
light) from approximately the size of the Earth to about
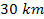 in radius, creating a proto-neutron star. The collapse is halted by
the short-range repulsive nuclear interactions. Note that according
to the UG theory, short-range nuclear interactions are driven by
repulsive zones of the UG gravitational equation 2-1-1 at distances
of
in radius, creating a proto-neutron star. The collapse is halted by
the short-range repulsive nuclear interactions. Note that according
to the UG theory, short-range nuclear interactions are driven by
repulsive zones of the UG gravitational equation 2-1-1 at distances
of
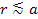 . .
Just before the initial stage of stellar or galactic formation, when
the Brownian pressure created by the gas particles can no longer
balance the gravitational force and the collapse of a gas cloud is
set in motion, there are no central superheavy particles of
substantial mass, and the potential energy curve of a test particle
of mass
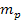 resembles the Newtonian potential energy (displayed by the blue curve
in figures 7-1a and 7-1b). As the density of matter, the temperature
and the pressure within the core of the collapsed star or galaxy
increase substantially following each stage of collapse, the
prevalence and the mass of the largest SHPs increase substantially,
in accordance with postulate IV. With the production of more massive
SHPs, the resultant potential energy of the object (presented by the
violet curve) begins to increase and to depart from the Newtonian
curve. Eventually, as long as the initial cloud is sufficiently
massive, the pressure and temperature at its core will build up to
high levels, where the production of superheavy particles yields an
adequate number
resembles the Newtonian potential energy (displayed by the blue curve
in figures 7-1a and 7-1b). As the density of matter, the temperature
and the pressure within the core of the collapsed star or galaxy
increase substantially following each stage of collapse, the
prevalence and the mass of the largest SHPs increase substantially,
in accordance with postulate IV. With the production of more massive
SHPs, the resultant potential energy of the object (presented by the
violet curve) begins to increase and to depart from the Newtonian
curve. Eventually, as long as the initial cloud is sufficiently
massive, the pressure and temperature at its core will build up to
high levels, where the production of superheavy particles yields an
adequate number
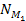 and mass
and mass
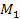 of a dominant SHP type to form a barrier that is capable of
deflecting inward-drifting matter, thereby preventing the matter from
penetrating the galactic disk. This will occur when
of a dominant SHP type to form a barrier that is capable of
deflecting inward-drifting matter, thereby preventing the matter from
penetrating the galactic disk. This will occur when
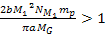 (see figures 7-1a and 7-1b). Since the transition to substantially
larger SHPs takes place during a sudden and relatively short period
of collapse, the rise of the barrier is almost instantaneous. As the
barrier emerges, the slope of the potential energy, located between
the newly formed
(see figures 7-1a and 7-1b). Since the transition to substantially
larger SHPs takes place during a sudden and relatively short period
of collapse, the rise of the barrier is almost instantaneous. As the
barrier emerges, the slope of the potential energy, located between
the newly formed
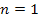 outer maximum contour and the adjacent external minimum (at
approximately
outer maximum contour and the adjacent external minimum (at
approximately
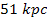 and
and
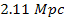 respectively in figures 7-1a to 7-1c) becomes negative.
Consequently, gas and other ordinary matter objects orbiting within
this distance range are suddenly subjected to a strong repulsive
force and ejected outward in the direction of the external minimum.14
As the volume of matter within the given distance range is emptied
out, a large void is formed. At distances exceeding the outer
minimum, the object’s potential energy curve converges toward
its Newtonian curve, thereby attracting ordinary matter and allowing
for a continuous inward flow of matter. However, the vast majority
of the inward flowing matter cannot penetrate the barrier and is
instead deflected toward the outer minimum contour, where new centers
of collapse may form, resulting in the fragmentation of the galactic
entity into a series of sister galaxies. The same process is repeated
again and again as the number of sister galaxies increases and the
area covered by them expands outwards.
respectively in figures 7-1a to 7-1c) becomes negative.
Consequently, gas and other ordinary matter objects orbiting within
this distance range are suddenly subjected to a strong repulsive
force and ejected outward in the direction of the external minimum.14
As the volume of matter within the given distance range is emptied
out, a large void is formed. At distances exceeding the outer
minimum, the object’s potential energy curve converges toward
its Newtonian curve, thereby attracting ordinary matter and allowing
for a continuous inward flow of matter. However, the vast majority
of the inward flowing matter cannot penetrate the barrier and is
instead deflected toward the outer minimum contour, where new centers
of collapse may form, resulting in the fragmentation of the galactic
entity into a series of sister galaxies. The same process is repeated
again and again as the number of sister galaxies increases and the
area covered by them expands outwards.
Section VII-6: UG
Repulsion and the Generation of Stellar Novae and Supernovae
A similar process may explain what initiates the sudden massive
expanding shell of gas and the high levels of radiation generated by
stellar novae and supernovae. A sudden and drastic increase in the
brilliance of a star is characteristic of a nova, where stellar
explosion causes the star to become 10,000 to 100,000 times brighter
than the Sun, and the cataclysmic supernova, where the exploding star
can become billions of times as bright as the Sun before fading out
of view. At its maximum brightness, the exploded star of the
supernova may outshine the entire galaxy. Both novae and supernovae
are characterized by a tremendous rapid brightening lasting few
weeks, followed by slow dimming, and both show spectroscopically
blueshifted emission lines, which imply that hot gases are blown
outward. It is yet unknown how the collapse of a dying star creates
an explosion that generates a massive outflow of gas and matter.
According to the fourth UG postulate, a significant increase in the
temperature and pressure of a stellar core leads to the sudden
creation of SHPs of significantly larger mass. A large and abrupt
increase in temperature and pressure occurs during the initial
collapse of the molecular cloud when the star is born, or at various
stages of the stellar life cycle described in section VII-5. The
initial collapse of a star results in a significant increase in
temperature and pressure within the central core, which may produce
pairs of substantially massive superheavy particles and
anti-particles. 15
The birth of larger SHPs almost instantaneously elevates the
potential energy curve, creating a barrier (for example, see the
transition from the blue curve to the violet curve of figures 7-1a
and b). Following the discussion of the previous section, the newly
formed barrier produces a sudden massive expanding shell of gas,
which drives out the vast amount of ordinary matter previously
located between the newly formed
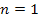 maximum and the newly formed external minimum. As the temperature in
the collapsing core becomes sufficiently elevated, the collapse of
the star is halted by the hydrogen burning process, producing higher
temperatures and increasing the outward pressure, thus balancing the
inward gravitational force within the star. When its supply of
hydrogen is nearly depleted, the collapse of the star is resumed.
Energy released during this second collapse allows for the production
of even larger SHPs, as the temperature and pressure within the
stellar core are increased. Hence, the radius of the
maximum and the newly formed external minimum. As the temperature in
the collapsing core becomes sufficiently elevated, the collapse of
the star is halted by the hydrogen burning process, producing higher
temperatures and increasing the outward pressure, thus balancing the
inward gravitational force within the star. When its supply of
hydrogen is nearly depleted, the collapse of the star is resumed.
Energy released during this second collapse allows for the production
of even larger SHPs, as the temperature and pressure within the
stellar core are increased. Hence, the radius of the
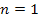 maximum contour, which is proportional to the dominant SHP of mass
maximum contour, which is proportional to the dominant SHP of mass
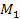 ,
and the radius of the adjacent external minimum, which is dependent
on ,
and the radius of the adjacent external minimum, which is dependent
on
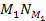 ,
are shifted outward, resulting in a significantly expanded barrier.
The new, extended barrier once again triggers a sudden massive
expanding shell of gas. This process is repeated through the series
of collapses. ,
are shifted outward, resulting in a significantly expanded barrier.
The new, extended barrier once again triggers a sudden massive
expanding shell of gas. This process is repeated through the series
of collapses.
The creation of superheavy particles of greater mass produces a
larger number of narrow minima within a shell contained between any
two successive minima of the former dominant SHP type, resulting in
an enormous number of local collapses toward the new set of minima.
This process releases a vast amount of energy in the form of
radiation, which together with the massive expanding shell of gas
produced by the outer barrier, may explain the phenomenon of a nova
or supernova.
A star that has experienced several stages of novae or supernovae is
likely to have exhausted a majority of its core hydrogen (and
possibly other light elements) and to produce heavier elements. Such
a star is also likely to have already shed most of its outer layers
via prior novae or supernovae or by its stellar wind (see section
VI-2). Therefore, in the later stages of a supernova, a star is
likely to lack the spectral lines of the lightest elements, while
demonstrating a higher abundance of heavier elements in its spectrum,
which may explain the various classifications of supernovae.
Section VII-7: The
Fragmentation of a Galactic Entity and the Creation of
Galactic Substructures
The creation of a series of
distinct galactic entities
by the collapse of a gas cloud was discussed in section VII-5. In
this section, the interplay between attractive and repulsive zones
within any galactic entity of a size larger than a typical galaxy
(typically of larger than 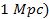 will be shown to provide a possible explanation for the fragmentation
of a galactic entity into a group or a cluster of galaxies.
will be shown to provide a possible explanation for the fragmentation
of a galactic entity into a group or a cluster of galaxies. Assume,
for example, that a specific galactic entity (the “parent
entity”) produced by the collapse of a gas cloud is described
by the same parameters used in figures 7-1a to 7-1c, with the
exception of 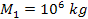 and
and 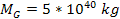 ,
and adheres to the same set of assumptions. The series of maxima and
minima of the potential energy curve of the parent entity is
demonstrated in figures 7-2a and 7-2b. As the density of matter in
the vicinity of the minima becomes elevated, some of the minima
develop into secondary centers of collapse, creating stars
or smaller “offspring” galaxies,
which generate sufficiently large SHPs of their own to produce a
barrier. The secondary stars
or galaxies
consequently become locked to external drifting matter, diverting
nearby matter to collapse at neighboring local minima.16
As a result, a series of interconnected stars,
galaxies or even
galactic groups,
clusters or superclusters
are created at the minima, thereby fragmenting the matter within the
galactic entity into a series of substructures.
Note that the offspring substructures are separated into groups,
where each group occupies a different minimum contour produced by the
superheavy particles of
the parent
entity, and their disk planes should subsequently be oriented
tangentially to the respective minima of the galactic parent. ,
and adheres to the same set of assumptions. The series of maxima and
minima of the potential energy curve of the parent entity is
demonstrated in figures 7-2a and 7-2b. As the density of matter in
the vicinity of the minima becomes elevated, some of the minima
develop into secondary centers of collapse, creating stars
or smaller “offspring” galaxies,
which generate sufficiently large SHPs of their own to produce a
barrier. The secondary stars
or galaxies
consequently become locked to external drifting matter, diverting
nearby matter to collapse at neighboring local minima.16
As a result, a series of interconnected stars,
galaxies or even
galactic groups,
clusters or superclusters
are created at the minima, thereby fragmenting the matter within the
galactic entity into a series of substructures.
Note that the offspring substructures are separated into groups,
where each group occupies a different minimum contour produced by the
superheavy particles of
the parent
entity, and their disk planes should subsequently be oriented
tangentially to the respective minima of the galactic parent.
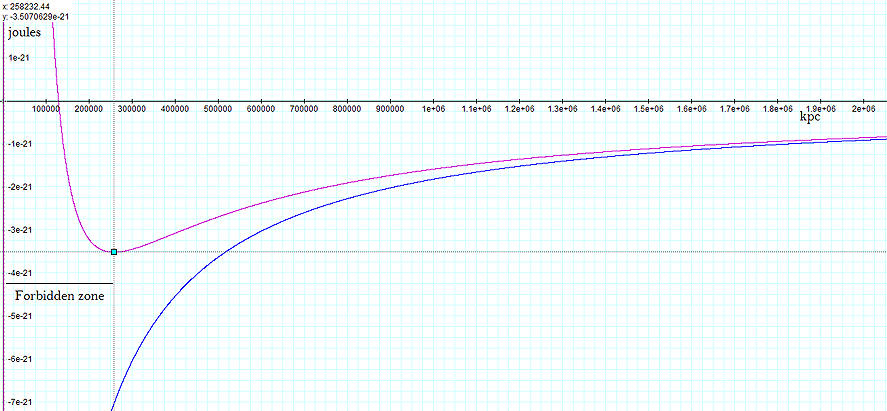
Figure
7-2a:Same
as figure 7-1a, using higher values of  and
and .
Rings collapse at
the minima to produce galactic substructures. .
Rings collapse at
the minima to produce galactic substructures.
Figures
7-2b:Same
as Figure 7-2a displayed on a larger distance scale. The
wide void (forbidden zone) which is shown to start at about 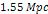 in Figure 7-2a is shown to extend all the way to
in Figure 7-2a is shown to extend all the way to 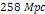 ,
where it starts to converge toward the ordinary matter Newtonian
curve (in blue). ,
where it starts to converge toward the ordinary matter Newtonian
curve (in blue).
Further
note that in figure 7-2b the void around the center of the parent
galaxy is nearly a perfect sphere with a radius of
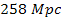 .
However, in a more realistic scenario, where the space within the
void is additionally influenced by other galactic entities and the
SHP groups move at relativistic speeds, the size and shape of the
void become distorted. Consequently, the void may contain few local
minima at which some galactic entities may form, and its geometry
does not demonstrate perfect spherical symmetry. However, the
average density of matter in the void is significantly reduced. .
However, in a more realistic scenario, where the space within the
void is additionally influenced by other galactic entities and the
SHP groups move at relativistic speeds, the size and shape of the
void become distorted. Consequently, the void may contain few local
minima at which some galactic entities may form, and its geometry
does not demonstrate perfect spherical symmetry. However, the
average density of matter in the void is significantly reduced. Finally,
it is important to note that the process described above, by which a
large galactic entity, or “parent” is broken into smaller
“offspring” substructures, does not take into account the
effect that the rotation of the large SHP groups may exert on the
fragmentation of the parent structure. The process of star formation
described in Chapters IV-1-2 and VI-4 may be extended to galactic
groups, clusters and superclusters, to explain the fragmentation and
distribution of galaxies within clusters.
Section
VII-8: Gravitational Repulsion Between Galaxies
The
rejection of ordinary matter by galaxies provides a mechanism by
which galactic entities may repel each other at distances larger than
the diameter of a supercluster. Repulsion between two galaxies will
be shown to persist over a large range of distances, starting at a
slightly larger distance than the oscillation range of ordinary
matter of mass
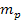 with
the dominant superheavy particles. The equation that describes the
interaction between the two galaxies is given by with
the dominant superheavy particles. The equation that describes the
interaction between the two galaxies is given by Equation
7-3
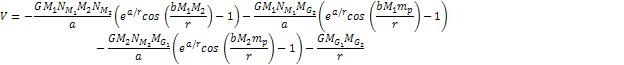
where
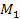 and
and
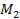 denote the respective masses of the dominant SHP types of the two
galaxies,
denote the respective masses of the dominant SHP types of the two
galaxies,
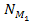 and
and
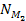 provide the total number of these SHPs in the respective galaxies,
and
provide the total number of these SHPs in the respective galaxies,
and
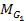 and
and
 are the total mass of the ordinary matter within each of the
galaxies. Note that the radii of the two galactic disks (which are
close to
are the total mass of the ordinary matter within each of the
galaxies. Note that the radii of the two galactic disks (which are
close to
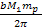 and
and
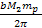 respectively) are assumed to be small relative to the distance
respectively) are assumed to be small relative to the distance
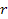 between their centers. The contributions of additional SHP groups
and of other heavenly objects are assumed to be negligible.
between their centers. The contributions of additional SHP groups
and of other heavenly objects are assumed to be negligible. The potential energy of the gravitational
interaction between two identical galactic entities using the same
structure and parameters as the latest example (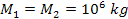 , ,
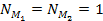 and
and
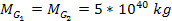 )
is depicted in figures 7-3a and 7-3b. The galaxies are shown to
repel each other at distances stretching between )
is depicted in figures 7-3a and 7-3b. The galaxies are shown to
repel each other at distances stretching between
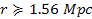 (which is the zonal oscillation range between the dominant SHPs and
ordinary matter of mass
(which is the zonal oscillation range between the dominant SHPs and
ordinary matter of mass
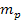 ,
denoted as ,
denoted as
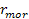 )
and )
and
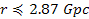 (which is the distance between the center of the galaxies and their
outermost potential energy minimum, denoted as
(which is the distance between the center of the galaxies and their
outermost potential energy minimum, denoted as
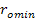 ).
In this example, the distance range of the repulsion between the
galaxies is of the order of about one third of the estimated size of
the observable universe. Note that the existence of roughly
spherical voids around each galactic entity must create a network of
non-randomly distributed galaxies that are positioned along two
dimensional sheets that form the walls of bubble-shaped regions of
space, in agreement with observations. ).
In this example, the distance range of the repulsion between the
galaxies is of the order of about one third of the estimated size of
the observable universe. Note that the existence of roughly
spherical voids around each galactic entity must create a network of
non-randomly distributed galaxies that are positioned along two
dimensional sheets that form the walls of bubble-shaped regions of
space, in agreement with observations.
As demonstrated in figure 7-3a, two isolated galaxies tend to cluster
together when the distance separating them is less than the zonal
oscillation range between their dominant superheavy particles and
ordinary matter of mass
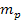 ,
denoted by ,
denoted by
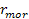 ,
causing them to gravitate toward a local minimum. When the distance
separating the two galaxies lies between ,
causing them to gravitate toward a local minimum. When the distance
separating the two galaxies lies between
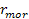 and
and
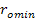 ,
the galaxies repel and accelerate away from each other. ,
the galaxies repel and accelerate away from each other.
The different terms of the force equation can be derived by computing
the gradient of equation 7-3, which can be shown to reduce
proportionally to either
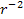 or to
or to
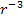 within the range
within the range
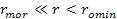 ,
and proportionally to ,
and proportionally to
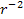 at distances
at distances
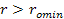 ,
where the effect of the SHP reduces significantly. At distances
greater than ,
where the effect of the SHP reduces significantly. At distances
greater than
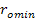 ,
the galaxies begin to attract each other and the UG equations
converge toward the Newtonian interactions between the ordinary
matter of the given galaxies. ,
the galaxies begin to attract each other and the UG equations
converge toward the Newtonian interactions between the ordinary
matter of the given galaxies.
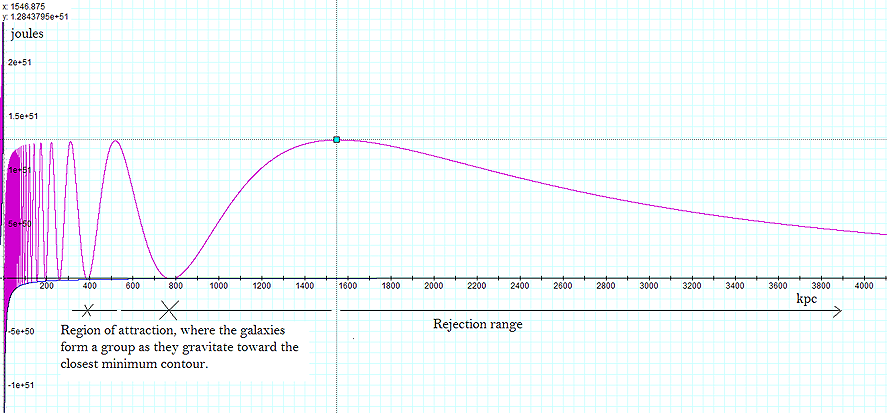
Figure
7-3a

Figure
7-3b
Figure
7-3:
The potential energy is displayed as a function of the intergalactic
distance due to the exclusive interaction of ordinary matter (blue
curve), or due to the interaction between ordinary matter and
superheavy particles
of two identical galaxies
using the parameters 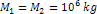 , ,
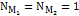 and
and 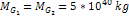 via equation 7-3. At distances of
via equation 7-3. At distances of 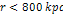 the galaxies
are bonded, creating a group (a). Between
the galaxies
are bonded, creating a group (a). Between 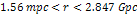 the galaxies
reject each other (b).
the galaxies
reject each other (b).
Consequently,
the velocity with which the two galaxies recede from each other
between
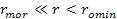 increases by an amount that is proportional to
increases by an amount that is proportional to
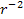 ,
and the velocity of two galaxies relative to each other converges
quite rapidly to their maximum receding velocity at ,
and the velocity of two galaxies relative to each other converges
quite rapidly to their maximum receding velocity at
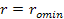 .
As the galaxies drift apart beyond the relative distance .
As the galaxies drift apart beyond the relative distance
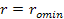 ,
the velocity at which they recede from each other is gradually
reduced by the attractive force between them. Whether the attractive
force at ,
the velocity at which they recede from each other is gradually
reduced by the attractive force between them. Whether the attractive
force at
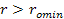 is sufficiently strong to eventually stop their motion away from each
other depends on the value of their potential plus kinetic energy at
is sufficiently strong to eventually stop their motion away from each
other depends on the value of their potential plus kinetic energy at
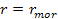 .
A positive initial energy indicates that the galaxies will continue
to recede to infinity, whereas a negative initial energy implies that
their motion away from each other will eventually come to a halt and
begin to accelerate in the reverse direction, back toward one
another. In the case of exactly zero energy, their receding will
continue forever as the relative distance between the galaxies
asymptotically approaches a maximum distance. .
A positive initial energy indicates that the galaxies will continue
to recede to infinity, whereas a negative initial energy implies that
their motion away from each other will eventually come to a halt and
begin to accelerate in the reverse direction, back toward one
another. In the case of exactly zero energy, their receding will
continue forever as the relative distance between the galaxies
asymptotically approaches a maximum distance.
Section
VII-9: The Expansion of the Universe
According to observation, the universe is expanding at an accelerated
rate. Invoking the Copernican principle leads to the conclusion that
the same isotropic expansion detected from Earth can be observed at
the present time anywhere else in the universe. In the following
discussion, the average size of a galactic cluster is denoted as
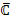 ,
the average distance between adjacent galactic clusters is denoted as ,
the average distance between adjacent galactic clusters is denoted as
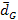 ,
and the average relative velocity of adjacent superclusters as they
recede from each other is given by ,
and the average relative velocity of adjacent superclusters as they
recede from each other is given by
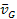 ,
where due to the Copernican principle, ,
where due to the Copernican principle,
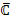 , ,
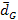 and
and
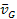 can be shown to be the same everywhere in the universe. Therefore,
an observer located in single galactic supercluster views adjacent
superclusters located at a distance of
can be shown to be the same everywhere in the universe. Therefore,
an observer located in single galactic supercluster views adjacent
superclusters located at a distance of
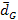 as receding at an average velocity of
as receding at an average velocity of
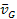 ,
superclusters located at a distance of ,
superclusters located at a distance of
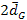 as receding at an average velocity of
as receding at an average velocity of
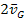 ,
and so on. This leads to the conclusion that two distant galaxies
should recede from each other at a speed proportional to the distance
between them. 171819 ,
and so on. This leads to the conclusion that two distant galaxies
should recede from each other at a speed proportional to the distance
between them. 171819
As shown in the previous section, two isolated galaxies tend to
cluster together when the distance separating them is shorter than
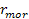 ,
to repel each other at distances between ,
to repel each other at distances between
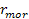 and
and
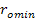 ,
or to attract each other at distances which exceed ,
or to attract each other at distances which exceed
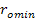 .
The velocity of a pair of galactic clusters as they recede from each
other was shown to increase, and to asymptotically approach the value
of their velocity at .
The velocity of a pair of galactic clusters as they recede from each
other was shown to increase, and to asymptotically approach the value
of their velocity at
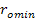 .
This may explain what causes the expansion of the universe. If the
matter of the universe is contained within a sphere of radius .
This may explain what causes the expansion of the universe. If the
matter of the universe is contained within a sphere of radius
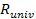 ,
where ,
where
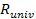 is of an order of less than or equal to the average
is of an order of less than or equal to the average
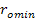 ,
the universe must expand in a uniform manner at an accelerating speed
that asymptotically approaches a constant expansion velocity.20 ,
the universe must expand in a uniform manner at an accelerating speed
that asymptotically approaches a constant expansion velocity.20
The UG theory further provides a mechanism to explain the observed
acceleration of the expansion of the universe. As a substantial
number of galactic cores enter into the next stage of collapse,
significantly more massive SHPs are produced, thereby increasing the
force with which the galactic entities repel each other. Invoking the
cosmological principle, this process must occur everywhere in the
universe at approximately the same time. Consequently, galaxies and
galactic clusters are expected to repel each other with increasing
force, escalating the expansion velocity of the universe.
Section
VII-10: Additional Comments about Unified Gravitation and the
Big Bang Model
The UG theory does not contradict, but can actually support the
model of a relatively small and dense universe that at some point in
time began to expand. However, there are two fundamental differences
between the UG and the Big Bang expansions. While the
expansion of the universe according to the Big Bang is assumed to
have started in a state of singularity, the
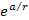 term of the maxima of the UG equation 2-1-1 prevents the
pre-expansion UG universe from becoming a point singularity.21
Consequently, the initial pre-expansion UG Universe is expected to
have been relatively small, yet infinitely larger than a
singularity, eliminating the problems that arise from the Big Bang
assumption that just prior to the beginning of the expansion, the
universe was in a state of infinite temperature and infinite
density, in which all known theories of physics would break down.
term of the maxima of the UG equation 2-1-1 prevents the
pre-expansion UG universe from becoming a point singularity.21
Consequently, the initial pre-expansion UG Universe is expected to
have been relatively small, yet infinitely larger than a
singularity, eliminating the problems that arise from the Big Bang
assumption that just prior to the beginning of the expansion, the
universe was in a state of infinite temperature and infinite
density, in which all known theories of physics would break down.
The
expansion of the universe, according to the UG theory, is driven by
the repulsive force between galactic entities, which results in an
accelerated expansion as long as the universe did not grow
sufficiently large for the distance between a majority of the
entities to become larger than
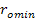 of the dominant SHPs in the universe.
of the dominant SHPs in the universe.
These fundamental differences allow a UG-based cosmological model to
avoid a number of problems presented by the Big Bang model. In
particular, the fact that unified gravitation provides for the
possibility of an accelerated expansion of the universe allows for
the amount of time elapsed since the start of the expansion to be
significantly larger than 14.5 billion years, resolving a potential
recurrence of the age dilemma. As aforementioned, the initial size
of the UG universe may have been extremely small, yet infinitely
larger than a point singularity, and the universe may be
substantially older than predicted by the Big Bang model.
Consequently, the different regions of the universe had significantly
more time to interact than previously estimated, thus avoiding the
horizon problem. In addition, the UG model accounts for the observed
tendency of matter within the universe to expand uniformly when
viewed on large spatial scale, and to cluster when viewed on small
spatial scale, therefore avoiding the problem of structure posed by
the Big Bang theory. Note that since the UG scenario provides for a
massive expansion of an extremely small initial universe, the theory
is also consistent with the discovery of an almost uniform cosmic
microwave background and with the theory of Big Bang
nucleosynthesis. Finally, the expansion of the universe according to
the UG theory is driven by the repulsive forces between massive SHPs
and ordinary matter, rather than relying on the
Freidman-Lemaitre-Robertson-Walker metric. Thus, the requirement
that the density of matter and energy in the universe be equal to a
critical density (within one part in
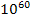 according to the current Big Bang Theory) is eliminated, thereby
avoiding the flatness problem. Consequently, the UG model does not
need to rely on the assumption that an inflation process occurred in
the early stages of the universe expansion, nor does it require the
presence of dark matter and dark energy, and may thus provide a
significantly simpler and potentially more stable theory than the
current cosmological model.
according to the current Big Bang Theory) is eliminated, thereby
avoiding the flatness problem. Consequently, the UG model does not
need to rely on the assumption that an inflation process occurred in
the early stages of the universe expansion, nor does it require the
presence of dark matter and dark energy, and may thus provide a
significantly simpler and potentially more stable theory than the
current cosmological model.
It is further important to address what could have initiated the
dramatic expansion of the universe. The UG explanation may involve a
process similar to the processes described earlier in this chapter
for the formation and dynamics of galactic entities. Consider, for
example, a universe initially composed of a uniform cloud of gas as
it begins to collapse toward its center, toward creating a single
high-density core. As the production of sufficiently massive
superheavy particles locks the galaxy disk to ordinary matter, excess
matter is diverted to nearby secondary centers of collapse,
generating a subset of galaxies. As the process is repeated, the
collapsing universe becomes filled with galactic clusters and
superclusters. Over time, the burning of hydrogen22
is depleted and a second collapse of the galactic core ensues,
resulting in the generation of heavier SHP types. At later stages of
collapse, the production of sufficiently massive superheavy
particles may create repulsion between clusters of galaxies, thus
halting the collapse of the universe and initiating an expansion via
the mechanisms described in sections VII-8 and VII-9. Eventually,
the distance between neighboring clusters will approach the average
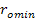 ,
and the effect of superheavy particles on the interaction between
galactic clusters will become negligible. Consequently, at this
point, the universe is expected to once again become compatible with
the general theory of relativity. In cases where the amount of
energy in the universe is insufficient to allow for continuous
expansion, the universe may begin to contract. However, the
existence of massive SHPs near the cores of galactic entities will
prevent a full collapse, and the density of the universe may begin to
oscillate around its average. This may occur as long as the
population of massive superheavy particles remains stable over time.
In case of significant decline in the SHP population, the universe
will begin to collapse and the process described above will begin a
new cycle. ,
and the effect of superheavy particles on the interaction between
galactic clusters will become negligible. Consequently, at this
point, the universe is expected to once again become compatible with
the general theory of relativity. In cases where the amount of
energy in the universe is insufficient to allow for continuous
expansion, the universe may begin to contract. However, the
existence of massive SHPs near the cores of galactic entities will
prevent a full collapse, and the density of the universe may begin to
oscillate around its average. This may occur as long as the
population of massive superheavy particles remains stable over time.
In case of significant decline in the SHP population, the universe
will begin to collapse and the process described above will begin a
new cycle.
Section
VII-11: The Galactic Halo and the Transition From a Spiral to
an Elliptical Galaxy
The rotation of a galaxy (as well as the rotation of its SHP groups)
tends to confine stars and matter within its galactic disk. As
discussed, the size of the galactic disk is determined by the radius
of the second minima
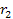 and is given approximately by
and is given approximately by Equation
7-11-1 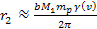
This
equation can also be used to estimate the mass of the dominant SHP
type. Assuming that the average radius of a galactic disk
of a spiral galaxy
extends approximately to 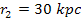 and that
and that 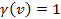 provides that
provides that 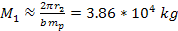 .
The same logic used in
sections VII-4, 5, and 8 for determining the repulsion between
galaxies can be applied
to stellar systems, leading to the conclusion that stars
may repel each other at certain distances. Hence, the number of
stars that can be
compressed into the galactic disk
is limited. Consequently, in a galaxy containing an excess number of
stellar systems that cannot be compressed into the disk must assume
orbits within the halo.
To quantify this statement, the maximum number of stars
that may be contained within the galactic disk
is of the order of .
The same logic used in
sections VII-4, 5, and 8 for determining the repulsion between
galaxies can be applied
to stellar systems, leading to the conclusion that stars
may repel each other at certain distances. Hence, the number of
stars that can be
compressed into the galactic disk
is limited. Consequently, in a galaxy containing an excess number of
stellar systems that cannot be compressed into the disk must assume
orbits within the halo.
To quantify this statement, the maximum number of stars
that may be contained within the galactic disk
is of the order of 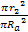 and the maximum quantity of stars
contained in the halo
is of the order of
and the maximum quantity of stars
contained in the halo
is of the order of 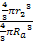 respectively, where
respectively, where 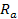 is the average shortest distance between neighboring stars
(therefore, the average stellar repulsion distance). In the case of
a galaxy with
is the average shortest distance between neighboring stars
(therefore, the average stellar repulsion distance). In the case of
a galaxy with 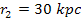 and
and 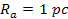 ,
the approximate maximum number of stars
within the galactic disk
and halo are ,
the approximate maximum number of stars
within the galactic disk
and halo are 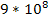 and
and 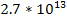 stars respectively.23
stars respectively.23 The size and mass of a
galaxy is determined by the mass of its dominant superheavy
particles. Following
the discussion of sections VII-4 and 5, the galaxy will eventually
become locked to ordinary matter by the production of large SHPs, and
the inflow of the gas which fuels the production of new stars
will practically cease. Over time, the supply of interstellar gas
within the galaxy will become depleted, as interstellar gas is used
for the production of new stars,
or is ejected from the galaxy in the form of galactic wind
(see section VI-2). The resultant galaxy is expected to contain
little or no cool interstellar gas or dust, and the majority of its
stars are expected to
reside within its halo.
Furthermore, the galaxy is expected to appear to have no stellar
disk, and as little or no new stars
are produced, its stellar population is expected to consist of older
stars. These
characteristics are widely observed in the elliptical classification
of galaxies. Between the time that the
galaxy becomes locked to ordinary matter and the depletion of its
interstellar gas, a significant amount of matter, energy and angular
momentum is lost in the form of galactic wind.
Consequently, the rotating core of the galaxy (which is the engine
of the galaxy) and its source of energy also lose energy and
momentum, as well as matter that is pumped out by the rotating
spiral. As a very limited amount of new gas enters the galaxy, the
central core is
deprived of additional fuel, and since its energy and momentum is
reduced, the rate of rotation of the galactic core
must slow down.24
As the central core loses some of its mass 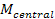 ,
and its rotation velocity reduces substantially ,
and its rotation velocity reduces substantially 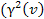 becomes closer to
becomes closer to  ,
the effect exerted on the velocity of the object by the SHP
and the central core, which is proportional to ,
the effect exerted on the velocity of the object by the SHP
and the central core, which is proportional to 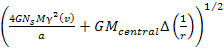 ,
decreases.25
On the other hand, as the number of stars
in the halo increases,
and the mass and rotational velocity of the central core and the
rotational velocity of the SHPs are reduced, the relative influence
of nearby matter on the object increases. Consequently, the galaxy
rotation curve may deviate substantially from constant velocity. ,
decreases.25
On the other hand, as the number of stars
in the halo increases,
and the mass and rotational velocity of the central core and the
rotational velocity of the SHPs are reduced, the relative influence
of nearby matter on the object increases. Consequently, the galaxy
rotation curve may deviate substantially from constant velocity.
Section
VII-12: Elliptical Morphology and Properties of Elliptical
Galaxies
The elliptical shape of a
galaxy is known not to correlate well with the rotation of the galaxy
as a whole (Caroll
& Ostlie, 2007, p. 988).
A possible reason for the elliptical shape of the galaxy is
that relativistic SHP groups distort the otherwise circular
equi-potential contours into elliptical ones, in which case the level
of ellipticity depends mainly on the velocity of the SHP groups.
For the simple case of a galaxy containing a single SHP
type of mass 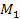 ,
the axes of the ,
the axes of the 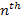 minima are given by
minima are given by
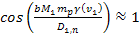 ,
or for the outermost substantial minimum, by ,
or for the outermost substantial minimum, by 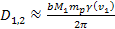 . . The apparent major axis 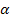 is given by
is given by 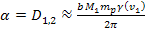 (where the velocity of the SHP group at the time of emission is
perpendicular to the distance between the location of the emission
and the location of interception of the gravitational signal by the
orbiting matter) and
the apparent minor axis
(where the velocity of the SHP group at the time of emission is
perpendicular to the distance between the location of the emission
and the location of interception of the gravitational signal by the
orbiting matter) and
the apparent minor axis 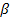 is given by
is given by 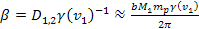 (where the given velocity and the distance are parallel). Therefore,
the observed ellipticity can be defined as
(where the given velocity and the distance are parallel). Therefore,
the observed ellipticity can be defined as 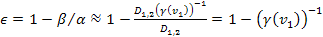 .
The largest ellipticity observed is approximately .
The largest ellipticity observed is approximately 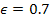 ,
suggesting that ,
suggesting that 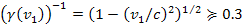 ,
or ,
or 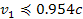 .
Note that in the more realistic case of multiple SHP
groups rotating on different rotational planes, the elliptical galaxy
may be triaxial without a single preferred axis of rotation. .
Note that in the more realistic case of multiple SHP
groups rotating on different rotational planes, the elliptical galaxy
may be triaxial without a single preferred axis of rotation.
Section VII-13:
The Boxiness vs. Diskiness of Elliptical Galaxies
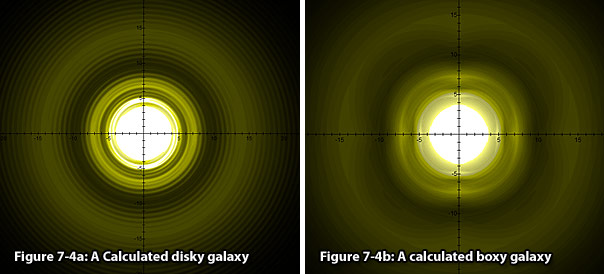
Figures
7-4a and 7-4b: A
calculated disky galaxy (7-4a) drawn using 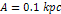 and a calculated boxy galaxy (7-4b) drawn using
and a calculated boxy galaxy (7-4b) drawn using 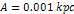 .
Both galaxies share the
parameters .
Both galaxies share the
parameters 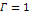 , ,
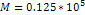 , ,
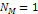 , ,
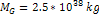 and and 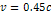 . .
Ralf Bender, Jean-Luc Nieto
and their collaborators proposed that many of the characteristics of
elliptical galaxies are
related to the degree of boxiness or diskiness that their isophotal
surfaces demonstrate (Bender,
1992). It
remained unclear, however, why a small portion of elliptical
galaxies present a boxy
appearance, while a majority of elliptical galaxies
are disky. Figure 7-4b (calculated via equation 4-1-1a) demonstrates
that a galaxy may take on a boxier appearance when the distance 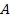 is selected to be sufficiently small for a superheavy particle group
moving at a relativistic velocity relative to the center of the
galaxy. With
is selected to be sufficiently small for a superheavy particle group
moving at a relativistic velocity relative to the center of the
galaxy. With 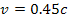 and
and
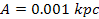 ,
the isophotal surfaces in figure 7-4b demonstrate clear departure
from elliptical morphology, particularly with increasing proximity to
the galaxy center. Increasing ,
the isophotal surfaces in figure 7-4b demonstrate clear departure
from elliptical morphology, particularly with increasing proximity to
the galaxy center. Increasing
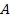 to
to
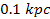 in figure 7-4a modifies the morphology of the galaxy into a more
spherical, or disky morphology.
in figure 7-4a modifies the morphology of the galaxy into a more
spherical, or disky morphology.
1
A free falling object is an object that is influenced exclusively by
the gravitational force.
2
The UG theory prevents the possibility of singularity (see section
VII-2). 3
One parsec (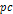 )
is equal to about )
is equal to about 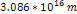 ,
and ,
and 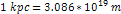 4
For further information, see Chapter VIII. 5
In general relativity the term ‘local frame’ refers to a
conceptual set of standardized clocks and measuring rods, which are
also subjected to acceleration by the local gravitational field. 6
This may be the case for galactic jets, pulsars or any plasma. 7
This is true for any massive object composed exclusively of ordinary
matter. 8
The term “galactic entity” refers to either a single
galaxy, or to a galactic group (containing 2 to 50 galaxies),
galactic clusters (containing 50 to 1000 galaxies),
or galactic superclusters
(containing more than 1000 galaxies).
9
The same mechanism should exist in stellar systems, and may also
exist in planets 10
A “drifting” particle describes a particle with a total
potential plus kinetic energy of close to  that begins its approach toward the galaxy from a very large
distance with a negligible amount of kinetic energy.
that begins its approach toward the galaxy from a very large
distance with a negligible amount of kinetic energy. 11
At distances exceeding the zonal range
of the superheavy particles
with ordinary matter, the UG contribution of the SHPs is negligible
compared with the contribution of the galaxy’s ordinary
matter. 12In terms of the more general
equation 4-1-1a, the parameters used are  , ,
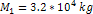 , ,
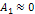 , ,
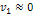 , ,
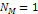 , ,
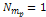 and and 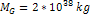 . .
13A forbidden zone is defined as a
spherically symmetric volume of space around the center of a galaxy
in which the orbit of an object composed exclusively of ordinary
matter cannot be completely confined. 14
For simplicity, it is assumed that the galaxy’s potential
energy is dominated by a single group of SHPs and by its ordinary
matter. Therefore the maximum associated with 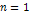 is well-defined.
is well-defined. 15
The newly generated superheavy particles
are ejected from the central core
and accelerated to relatively high (relativistic) velocities
according to the process described in Chapter III-3 (note that a
similar mechanism may solve the long-standing puzzle of why the
compact object remaining after a supernova explosion is given a
velocity kick away from the core. Observations
over the last decade have shown that at birth neutron stars
receive a large velocity kick of the order of a hundred to a
thousand 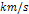 (Hoflich,
Kumar & Wheeler, 2004).
Within the UG theory, the compact object may be a superheavy
particle generated in or near the galactic central core, with
sufficient kinetic energy to be ejected out of the central core
together with ordinary matter trapped by the SHP
zones. (Hoflich,
Kumar & Wheeler, 2004).
Within the UG theory, the compact object may be a superheavy
particle generated in or near the galactic central core, with
sufficient kinetic energy to be ejected out of the central core
together with ordinary matter trapped by the SHP
zones. 16
Note that the locations of the minima are determined by both the
parent entity and its offspring substructures. 17
Note that according to this statement, distant galaxies
are expected to recede from each other at superluminal velocity.
Superluminal velocities do not contradict the special theory of
relativity in this case, as there is no global inertial system at
which the velocity between the two galaxies
can be measured. 18
Note that the expansion of the universe,
according to the current standard model
of cosmology, is viewed as the expansion of the intervening space
between galaxies, rather
than as the expansion of galaxies
into an empty space. 19
In accordance with general relativity and the cosmological
principle, there is
nothing external to the whole system of matter in the universe. 20
However, the speed of two given galactic clusters is likely to vary
from the speed expected for the same clusters in isolation, as each
one of them is affected by the entire mass of the universe, and not
only by the other cluster. 21
See the discussion of singularity
in Chapter II and in section VII-2 of this chapter. 22
Recall that the hydrogen burning process is responsible for stopping
the initial collapse and thereby prevents the galactic core
from collapsing further. 23
Note that an increase in 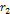 ,
according to the UG theory, would provide more space for stars
to form within the galactic disk.
However, the value of ,
according to the UG theory, would provide more space for stars
to form within the galactic disk.
However, the value of 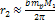 is determined by the mass of the dominant superheavy particles
in the galactic center. Therefore, as the initial stellar quantity
was substantially lower than
is determined by the mass of the dominant superheavy particles
in the galactic center. Therefore, as the initial stellar quantity
was substantially lower than 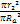 (or
(or 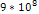 in
the current example), the rotation of the galaxy confined all stars
located within the in
the current example), the rotation of the galaxy confined all stars
located within the 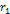 maximum contour to the galactic disk,
while stars located
beyond this maximum were ejected from the galaxy in the form of
galactic wind (see
section VI-2).
maximum contour to the galactic disk,
while stars located
beyond this maximum were ejected from the galaxy in the form of
galactic wind (see
section VI-2). 24
Note that upon the occurrence of another stage of collapse, the
rotation rate of the galactic core
will increase substantially. 25According
to equation 6-5.
|



