At any given time, our knowledge of the natural world can be
summarized by means of physical laws. These laws are used to
construct mathematical models to describe essential aspects of an
existing physical system. As we broaden our domain of observation, we
must constantly verify whether these models, and their embedded laws,
continue to be valid. Ideally, an existing model should be
repeatedly tested and critiqued via an iterative process, in which
new experiments are conducted and their results compared with the
predictions of the mathematical model. A model that remains
consistent with all measurements and observations will gain in
status. In cases where its predictions deviate from the results of
new experiments, a model must be adjusted to fit both the prior and
the new sets of results. As science progresses and the number of
iterations grows, an existing model may become increasingly difficult
to adjust. Eventually a paradigm shift might offer radical
simplification, and a new model may emerge to replace the old one.
This process should be governed by the principle of Occam’s
Razor, which states that the explanation of any phenomenon should
make as few assumptions as possible. This principle can be expressed
as, ‘If all other things being equal, the simplest solution is
the best.’ In accordance with Occam’s Razor, most
successful models are initially developed with a relatively simple
structure of few variables governed by few equations. However, in
most cases there is a clear trade-off between the simplicity of a
model and its accuracy. As new measurements deviate from the model’s
predictions by an amount that cannot be discounted simply as
measurement noise or measurement error, the model must be adjusted in
order to fit reality. Inevitably, this iterative process increases
the model’s complexity. Therefore, it is important not only to
verify (after each iteration) that the modified model is consistent
with the entire database of new and old experiments, but also to
substantiate that the model is still consistent with Occam’s
Razor, namely that the modified model is still the simplest model
that explains the behavior of the given physical system. This second
criterion, however, is often overlooked or lost in the process.
One of the most fundamental and powerful models used in physics
combines Newton’s classical mechanics, which describes the
relationship between force and the motion of bodies, and Newton’s
law of universal gravitation. Newton based his theory on three
simple postulates and two simple equations that have since been
demonstrated to provide an efficient and astonishingly accurate model
of most ordinary mechanical situations. Over 200 years of scientific
advances transpired before measurements started to suggest the need
for a departure from the Newtonian model.
Newton’s law of universal gravitation and his laws of motion
were based on prior work done by Galileo and Kepler. Johannes
Kepler, a German mathematician, studied observations of planetary
dynamics tabulated by the Danish astronomer Tycho Brahe and developed
an ad hoc mathematical model to describe the empirical observations
via three laws of planetary motion.1
Kepler’s laws provided a clear blueprint with which an
astronomer of the time could calculate and predict the location and
the periodicity of planets in the Solar System. While his achievement
was incredibly important, Kepler’s mathematical laws were
empirical in nature, and were not derived from any basic underlying
principles. The rationale and explanation of the theoretical
principles driving these rules emerged over half a century later with
Newton’s publication of his Philosophiae Naturalis Pricipia
Mathematica.
As Newton’s mathematical model was based on a more profound
understanding of fundamental principles, the shortcomings of the
Keplerian model became apparent. Kepler’s laws were found to
be inaccurate when the mass of an orbiting object is not negligible
in comparison to the mass of the object being orbited. Furthermore,
Kepler’s laws did not deal with situations in which the smaller
body is moving faster than the escape velocity, as in the case of
comets. Under such circumstances, the small body trajectory becomes
an open parabolic or hyperbolic orbit, rather than a closed
elliptical orbit. In addition, Kepler’s laws assumed a
two-body system and could not be applied accurately to systems
containing three or more bodies.2
Newton’s insight therefore provided a simpler and more
accurate way of calculating planetary trajectories, which not only
resolved the limitations of Keplerian dynamics, but also
substantially increased the scope of applications covered by the
model.
The basic framework for Newton’s theory was also inspired by
the work of Italian astronomer Galileo Galilei, introduced in 1638.
Before Galileo, ideas about the motion of bodies were based on
Aristotle’s assertion that the natural state of a body was to
be at rest and that a resting body will move only if driven by a
force or impulse. Aristotle further intuited that a heavy body
should fall faster than a lighter one, as the heavy body should by
nature experience greater pull toward the earth. Galileo put these
notions to a test. By rolling balls of different weights down a
smooth slope, Galileo created an effect similar to bodies falling
vertically, and found that contrary to Aristotle’s predictions,
the speed of all bodies increased at the same rate regardless of
their mass (as long as air resistance and friction can be neglected).
In other words, the gravitational acceleration of an object is
independent of its mass. This idea led Einstein, almost three
centuries later, to his equivalence principle and to the development
of the general theory of relativity. Galileo’s experiment
further demonstrated that the effect of a force is to change the
speed of a body, rather than simply to set it in motion. It followed
that a body moving on a level surface will continue to travel in the
same direction at constant speed unless disturbed, a principle that
became Newton’s first law. Galileo also formed the principle
of Galilean relativity, stating that dynamical laws are precisely the
same when referred to in any non-accelerating frame of reference,
where reference frames travel at constant velocity relative to each
other. Hence, there is no experiment that can differentiate between
a system at rest and a system in uniform motion, and there is no
absolute motion or absolute rest state. This principle initially
provided the basic framework for Newton’s theory and later on
inspired Einstein’s special theory of relativity.
Newton’s original formulation of his laws of motion stated the
principle of Galilean relativity as one of five or six fundamental
laws. Later on, however, Newton adopted the notion of absolute space
and simplified his model to rely on only three independent laws:
Newton’s First Law: A particle will stay at rest
or continue to move at a constant velocity following a straight line
unless acted upon by an external unbalanced force.
Newton’s Second Law: Observed from an inertial
frame (a frame at rest or moving at constant velocity) the net force
on a particle is equal to the particle mass times its acceleration,
or
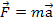 . .
Newton’s Third Law: Whenever a particle A exerts
force on a second particle B, B simultaneously exerts a force of same
magnitude in the opposite direction on particle A.
Newton then formulated a law to describe the gravitational force,
stating that two point objects of mass
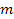 and
and
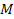 attract each other along the line that connects them via a force that
is proportional to the product of their masses divided by the square
of the distance
attract each other along the line that connects them via a force that
is proportional to the product of their masses divided by the square
of the distance
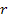 that separates them. Expressed mathematically,
that separates them. Expressed mathematically,
Equation
1-1
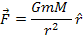
where
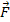 is the gravitational vector force applied on either point particle,
G is a gravitational constant, and
is the gravitational vector force applied on either point particle,
G is a gravitational constant, and
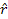 is the unit vector in the direction toward the other point object.
Newton’s gravitational force thus describes a central force,
which can also be stated as a conserving force that is derived from a
potential energy function
is the unit vector in the direction toward the other point object.
Newton’s gravitational force thus describes a central force,
which can also be stated as a conserving force that is derived from a
potential energy function
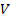 via
via
Equation
1-2
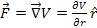 ,
where ,
where
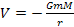
Remarkably,
just a few simple rules result in an extraordinarily powerful and
versatile theory that predicts the behaviors of macroscopic objects
with great accuracy, as long as their speeds are non-relativistic.
For his theory to work Newton had to assume, against his own judgment
and instincts, that gravity is instantaneous, or in other words that
the speed of gravity is infinite. Newton was also quite
uncomfortable with the notion implied by his equations that gravity
is an “action at a distance,” without direct contact
between the bodies involved.
While no mathematical model can exactly reproduce an actual physical
system, the Newtonian theory remained virtually unchallenged for over
200 years. That is, until Albert Einstein introduced his
revolutionary special theory of relativity, which provided a more
accurate model in the case of object velocities that approach the
speed of light, and his new gravitational theory, the general theory
of relativity, which resolved a number of shortcomings within
Newton’s theory of gravitation. Special relativity, and to a
larger extent general relativity, significantly increased the
mathematical complexity of both mechanical dynamics and gravitation,
resulting in a set of non-linear equations that often require
resolution via computer-based simulations. However, both theories
are complete and self-consistent theories based on strikingly simple
postulates. Special relativity relies on the principle of relativity
and also postulates that the speed of light is the same in all
inertial frames. General relativity relies on the principles of
special relativity and on the equivalence principle.3
Both theories converge to the Newtonian gravitational model in the
limiting case of slow velocities (in the case of special relativity)
or weak gravitational fields (in the case of general relativity),
where their equations approach Newton’s equations. Due to the
minimalistic nature of their assumptions, special relativity and
general relativity can be considered to comply with the spirit of
Occam’s Razor, regardless of their substantial computational
complexities. However, the simplicity of Newton’s model, and
the fact that the majority of known systems are non-relativistic,
make it the preferred choice for most applications. Therefore, in
spite of the somewhat reduced accuracy of the Newtonian model
relative to general relativity or special relativity, it is still the
most frequently used model in earthbound engineering applications, as
well as in most areas of space exploration.
As our domain of observation has broadened considerably in the recent
century, studies have begun to show significant inconsistencies
between observations and the predictions of both, Newton’s
theory and general relativity. Some of the new discoveries were
attributed to non-gravitational phenomena, as in the case of the
strong interaction between nucleons, which was classified as an
entirely new force unrelated to gravitation and became part of the
standard model. Other inconsistencies clearly related to
gravitation were reconciled by modification of the gravitational
model of the Universe in an iterative process, resulting in a
significant increase in the complexity of the overall gravitational
model. Ideally, every iteration step should have been tested to
uphold the following criteria:
1. Can the modified model explain, quantify and be consistent with
all prior known phenomena, as well as the new discoveries?
2. Is the modified model still the simplest one available? Or
alternatively, can it be replaced by an equally successful, yet
substantially simpler model?
The risk in the failure to uphold the second criterion is that even a
flawed model that agrees with all prior known phenomena can be
modified to agree with new contradicting data by simply increasing
the number of independent variables used, thus creating a more
complex and still flawed model. The best way to eliminate flawed
models, but by no account the easiest route to take, is by searching
and testing for simpler alternative models.
The current astronomical model of the universe, which describes the
motion of a system of gravitating bodies, is based on the general
theory of relativity (and therefore indirectly on the less complete
Newtonian theory). The amount of visible matter observed in
galaxies and galactic clusters is insufficient to explain the motion
of stars in galaxies, or the motion of galaxies within clusters. We
can therefore conclude that either the current understanding of
gravitation is incorrect, or additional non-visible matter must
exist. At present, most astrophysicists prefer the latter
explanation, and consequently a new variable of dark matter has been
added to the current paradigm. The addition of the dark matter
concept made possible the formation of a plausible model that is
consistent with observations without shaking the theoretical
foundation of the established gravitational model. Since
undetected, dark matter is believed to consist of non-baryonic matter
and to interact through the gravitational force. To fit observations,
dark matter must account for about 90% of the average galaxy mass,
and furthermore must dominate the mass of the galaxy up to several
hundred kiloparsecs from its center. However, no trace of dark
matter has ever been observed directly and no effects of such matter
can be measured within our own Solar System. The complexity of the
dark matter model, and the lack of direct observational evidence,
should raise the question of whether modification of the cosmological
model with the inclusion of dark matter still provides the simplest
possible model to explain the observed properties of galaxies as well
as stellar and galactic motions, or whether a simpler model exists.
Additional variables have been incorporated into the current accepted
cosmological model in a series of iterations geared to resolve
paradoxes related mainly to the Big Bang theory. The added variables
include the assumption of the existence of dark energy, which
together with dark matter brings the total amount of non-visible and
undetected matter in the universe to as large as 96%, as well as a
theory of inflation, which indicates that at some initial period of
time, space expanded at a rate much higher than the speed of light.
Newton never published the reasoning that guided him to his equation
of universal gravitation, and we can only speculate the process by
which he arrived at this final form, however, history provides us
with a clear sense of the information available to Newton at the
time. On no account could he have known about the phenomenon of
constant rotation curves in spiral galaxies, where stars travel
around the galactic center with roughly constant rotational speed,
rather than at a speed decreasing inversely to the square root of the
star’s radius of orbit. While Galileo had observed a system of
rings around Saturn prior to Newton’s work, its characteristics
were not yet understood. The difficulties of fully explaining
planetary rings within the Newtonian theory have since proved to be
formidable, as attested by the fact that almost 400 years later we
are still very far from understanding the root of their existence.
Newton did not have access to deep inelastic scattering experiments
that have since brought to light the behavior of particles on a
subatomic scale and could not have known about the existence of the
short-range strong forces between nucleons within the nucleus. Such
forces were later observed to be strong enough to overcome the
Coulomb rejection force between protons, and therefore must be
greater than
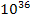 times the strength of the gravitational force predicted by Newton’s
formula, at nuclear distances of the order of
times the strength of the gravitational force predicted by Newton’s
formula, at nuclear distances of the order of
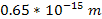 .
Although the strong force is considered as a separate force,
entirely distinct from gravitation, it appears to share some of
gravitation’s essential defining qualities. Similar to the
gravitational force, for instance, the subatomic force appears to be
(at least approximately) a central force between a pair of point-like
particles with strong dependency on the respective masses of the
interacting particles.4
An interesting yet speculative question is whether Newton would have
attempted to integrate the additional observed phenomena into his
theory of gravitation had the above information been available to
him? We can only suppose Newton’s course of action, but the
question that should be addressed and may be contemplated is whether
such phenomena, from long-range force interactions to force
interactions on a nuclear level, can be explained by a single
equation that provides a simpler and more accurate model than the
current paradigm. .
Although the strong force is considered as a separate force,
entirely distinct from gravitation, it appears to share some of
gravitation’s essential defining qualities. Similar to the
gravitational force, for instance, the subatomic force appears to be
(at least approximately) a central force between a pair of point-like
particles with strong dependency on the respective masses of the
interacting particles.4
An interesting yet speculative question is whether Newton would have
attempted to integrate the additional observed phenomena into his
theory of gravitation had the above information been available to
him? We can only suppose Newton’s course of action, but the
question that should be addressed and may be contemplated is whether
such phenomena, from long-range force interactions to force
interactions on a nuclear level, can be explained by a single
equation that provides a simpler and more accurate model than the
current paradigm.
In fact, there is a whole family of equations that, given the limited
observation technology available to Newton and for about 230 years
thereafter, would have provided virtually indistinguishable results
and predictions from those developed by Newton at the measured
distance ranges available at the time. However, on extremely small
scales, and in some cases on galactic or cosmic scale distances, the
predictions formulated by these equations may differ from each other,
and from the predictions of the Newtonian equation. These
distinctions could not have been addressed during Newton’s time
and would have been irrelevant to his reasoning, since the
alternative equations are slightly more complex and would have been
discounted in accordance with Occam’s Razor.
If a simpler model does exist, it is likely to be based on a modified
gravitational equation. To explore this notion, let us first analyze
some simple alternative equations for the gravitational potential
energy, starting with the exponential energy equation,
Equation
1-3
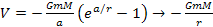 as
as
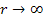
Note
that
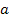 is a constant with a dimension of distance. For reasons that will
become apparent in the next chapter, a good choice for
is a constant with a dimension of distance. For reasons that will
become apparent in the next chapter, a good choice for
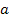 could be in the vicinity of
could be in the vicinity of
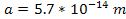 .
This will result in the following force equation: .
This will result in the following force equation:
Equation
1-4
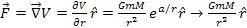 as
as
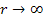
The choice made in equation 1-3 may seem odd and non-intuitive.
However, equation 1-3 is practically indistinguishable from Newton’s
equation of potential energy (1-2) at the distance range of
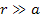 .
Similarly, at these distances, the results of equation 1-4 cannot be
distinguished from those of Newton’s equation of force (1-1).
Although the force in equation 1-4 is exponential, rather than
proportional to .
Similarly, at these distances, the results of equation 1-4 cannot be
distinguished from those of Newton’s equation of force (1-1).
Although the force in equation 1-4 is exponential, rather than
proportional to
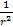 ,
the difference between the force calculated via equation 1-4 and the
Newtonian force calculated via equation 1-1 merely amounts to about
0.1% at a distance of ,
the difference between the force calculated via equation 1-4 and the
Newtonian force calculated via equation 1-1 merely amounts to about
0.1% at a distance of
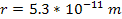 ,
which is the Bohr radius, or roughly the radius of the hydrogen
atom. At a distance of ,
which is the Bohr radius, or roughly the radius of the hydrogen
atom. At a distance of
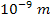 the difference reduces to about 0.0057%,
and at distances above one micrometer (
the difference reduces to about 0.0057%,
and at distances above one micrometer (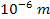 ),
there is virtually no difference between the two calculated
forces. In other words, if Newton had used the slightly more complex
equation 1-4 (or 1-3) rather than equation 1-1 (or 1-2), he would
have obtained the exact same results. Nevertheless, had the thought
of using an exponential function occurred to Newton, the inability at
the time to experimentally differentiate between the two sets of
equations would have most likely steered him toward the simpler
equation 1-1, in accordance with Occam’s Razor. While
equations 1-3 and 1-4 are also quite simple, they contain an
additional universal constant ),
there is virtually no difference between the two calculated
forces. In other words, if Newton had used the slightly more complex
equation 1-4 (or 1-3) rather than equation 1-1 (or 1-2), he would
have obtained the exact same results. Nevertheless, had the thought
of using an exponential function occurred to Newton, the inability at
the time to experimentally differentiate between the two sets of
equations would have most likely steered him toward the simpler
equation 1-1, in accordance with Occam’s Razor. While
equations 1-3 and 1-4 are also quite simple, they contain an
additional universal constant
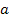 and require the calculation of an exponential function, which was not
an easy task in the pre-calculator era of the 17th
century.
and require the calculation of an exponential function, which was not
an easy task in the pre-calculator era of the 17th
century.
Today data is available on interactions at distances at which the
predictions of Newton’s equations of force and potential energy
differ from those of equations 1-4 and 1-3, and the results of the
two sets of equations are no longer identical within all measurement
ranges. Had Newton selected equation 1-3 (or 1-4) as his law of
gravitation, then three centuries later the discovery of a strong
nuclear force may have possibly been perceived as an additional
triumph for the theory of gravitation. After all, the newly
discovered strong force was found to be approximately a central
force5
between a pair of particles that is mainly dependent on the particle
masses, and to demonstrate explosive growth at the distances
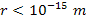 ,
just as predicted by equations 1-3 and 1-4 due to the explosive
growth of the exponential term ,
just as predicted by equations 1-3 and 1-4 due to the explosive
growth of the exponential term
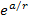 at distances
at distances
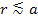 . .
The finding that a single mathematical equation may display behaviors
that resemble at least some key characteristics of the strong force
at extremely short distance ranges, while converging with Newton’s
gravitational equation at larger distances, does not necessarily
imply that the two forces are one and the same. However, such a
theory does not appear to have ever been considered. Instead, the
strong force became a part of an extensive new theory called the
standard model.6
Based on Newton’s law of gravitation, the standard model was
developed with the underlying assumption that the gravitational
force is negligible at atomic and sub-atomic distances.
Exponential equations such as 1-3 or 1-4 are not the only possible
alternatives to Newton’s gravitational equations 1-1 and 1-2.
Of interest are also equations of the type
Equation
1-5
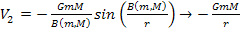 as
as
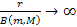
and
Equation
1-6
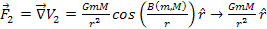 as
as
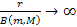
where
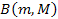 is either a constant or a function of the particle masses. Equations
1-5 and 1-6 provide a perfect Newtonian attractive force at distances
is either a constant or a function of the particle masses. Equations
1-5 and 1-6 provide a perfect Newtonian attractive force at distances
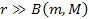 ,
where they become virtually indistinguishable from the Newtonian
equations. At shorter distances of ,
where they become virtually indistinguishable from the Newtonian
equations. At shorter distances of
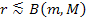 ,
the potential energy ,
the potential energy
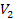 begins to oscillate between a series of constant maxima and minima (
begins to oscillate between a series of constant maxima and minima (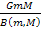 and
and
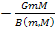 respectively), at which point the force can also become repulsive.
The cyclical nature of these equations may be functional in
addressing the cause of the ring and spiral structures demonstrated
in galaxies and planets, as well as for the shell structure and
resonances of the atom’s nucleus. However, in this form, these
equations are unlikely to be consistent with the strong force, since
it is not possible to find a function
respectively), at which point the force can also become repulsive.
The cyclical nature of these equations may be functional in
addressing the cause of the ring and spiral structures demonstrated
in galaxies and planets, as well as for the shell structure and
resonances of the atom’s nucleus. However, in this form, these
equations are unlikely to be consistent with the strong force, since
it is not possible to find a function
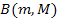 that can simultaneously provide the high amplitude required at short
distance ranges and the abrupt and explosive growth of the force at
the distance range of
that can simultaneously provide the high amplitude required at short
distance ranges and the abrupt and explosive growth of the force at
the distance range of
 . .
As
it turns out, neither equation 1-3 nor equation 1-5 can reproduce and
explain the entire range of observational data. However, merging
these two concepts will be shown to provide a simpler and more
accurate theory than the current paradigm, with the ability to
explain a large number of yet unexplained phenomena.
The hypothesis presented here, entitled the theory of unified
gravitation (UG), holds that the nuclear strong interaction and
gravitation are actually one and the same force, viewed at different
distance scales. This force is predominantly a central force between
a pair of fundamental particles,7
and can be derived from a central potential given by
Equation
1-7
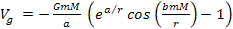
The
equation uses the gravitational constant , as well as two additional
universal constants,
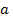 and and
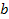 .
Variables .
Variables
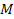 and
and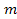 represent the respective masses of two particles, and
represent the respective masses of two particles, and
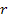 is the distance between the pair of particles.
is the distance between the pair of particles.
When
applied to objects consisting exclusively of ordinary particles at
distances significantly larger than 10 micrometers, the UG force equations developed in the first two
chapters will be shown to yield results indistinguishable from those
derived by Newtonian calculations within the experimental level of
reliability.8
However, when applied to much heavier particles, the results
obtained by the UG and Newtonian equations may diverge at much larger
distance ranges, and the UG potential and its derived force are able
to elucidate many thus far unexplained observations in the cosmic,
galactic, planetary and nuclear realms. The ability of larger
particles to form is demonstrated by high-energy collisions between
electrons and positrons, which have been shown to produce particles
that are more than 350,000 times their mass. Therefore, a secondary,
but essential assumption of the UG theory holds that the high
pressure and temperature conditions at the cores of large
satellites, planets, stars, and galaxies provide the energy and means
necessary to produce superheavy particles (SHPs) and to prevent their
decay.
The
present book is intended to introduce the theory of Unified
Gravitation (UG). It would be unreasonable to expect that the
capability of any new theory to provide better agreement in one
particular area is sufficient to challenge a well-established
fundamental theory that for centuries provided a clear picture of the
known universe. Therefore, the UG theory must be applied
successfully to the analysis of a wide range of phenomena in multiple
areas of physics. The purpose of this book, therefore, is to
demonstrate sufficient evidence of the viability and the advantages
of unified gravitation, in order to challenge and motivate the
physics community toward further testing.
The
first three chapters are dedicated to developing the UG postulates
and gravitational equations. The theory will subsequently be applied
on solar, galactic and cosmological scales to explain a broad
selection of observed phenomena. In the fourth and fifth chapters, a
simple UG-based model will be demonstrated to provide for a number of
the observed morphologies of astronomical systems. In Chapter IV, a
simple model will be employed
to reproduce a variety of complex morphologies observed in planetary
nebulae
and galaxies,
from bipolar structures in figure 4-4 to ring structures in figure
4-5, to simple spiral structures in figure 4-8 to flocculent spirals in figure 4-9.9

Figures
4-4d and 4-4e: A
comparison between a bipolar structure calculated by the UG equations
(figure 4-4d) and MyCn 18,
the hourglass nebula
(figure 4-4e). Image credit for figure 4-4e: R. Sahai and J.
Trauger, Photo AURA/STScl/NASA/JPL
(NASA photo # STScl-PRC96-07)
http://apod.nasa.gov/apod/ap020615.html.

Figure
4-5a: A UG calculated
image of a ring morphology
(on the left), compared with Hoag’s object and the planetary
nebula Abell 39.
Figure
4-5b: Hoag’s
Object, image credit:
NASA
and the Hubble Heritage Team (STScI/AURA) Acknowledgment: R.
Lucas(STScI/AURA)
http://www.nasaimages.org/luna/servlet/detail/NVA2~4~4~4753~105279:Hoag-s-Object--A-Strange-Ring-Galaxy.
Figure
4-5c: The Planetary Nebula Abell 39,
WIYN Observatory’s 3.5-m (138-inch) telescope at Kitt Peak
National Observatory, Tucson, AZ. Image credit: “NOAO/AURA/NSF.”
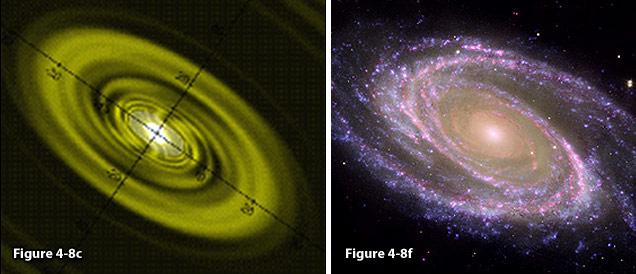
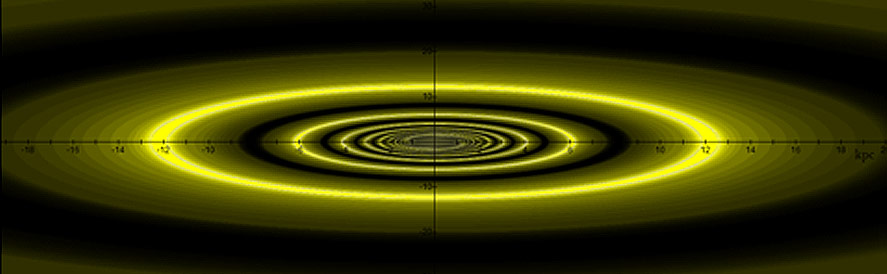
Figure
4-8e: A modeled galaxy
compared with the observed spiral galaxy
M81 (figure 4-8f).
Figure
4-8f: M81
image credit: NASA’s
Spitzer and Hubble space telescopes
and NASA’s Galaxy Evolution (NASA/JPL-Caltech/ESA
/Harvard-Smithsonian CfA),
http://www.nasa.gov/mission_pages/spitzer/multimedia/spitzer-20070604.html.

Figure
4-8i: NGC 4622,
image credit: G. Byrd, R. Buta, (Univ.Alabama,
Tuscaloosa), T. Freeman (Bevill
State College),
NASA
http://apod.nasa.gov/apod/ap040221.html.
Figure
4-8j:A
modeled spiral galaxy
compared with the observed galaxy NGC 4622
(figure 4-8i), which displays both trailing and leading spiral arms.

Figure
4-9a:A modeled spiral
galaxy compared with the
observed galaxy NGC 488
(figure 4-9b), demonstrating a flocculent
structure.
Figure
4-9b:NGC
488, image credit: Johan Knapen and Nik Szymanek, Isaac Newton group of telescopes;
http://www.ing.iac.es/PR/science/ngc488.html.

Figure
4-7c:
An infrared view of the Andromeda
Galaxy
taken by NASA’s
Spitzer
Space Telescope.
Image credit:
NASA/JPL-Caltech/K. Gordon (University of Arizona),
http://www.spitzer.caltech.edu/Media/releases/ssc2005-20/ssc2005-20a.shtml.
Figure
4-7d: A UG calculated
image of the Andromeda
Galaxy.
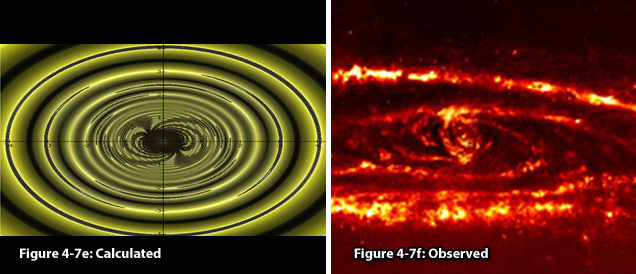
Figure
4-7e: Calculated
Figure 4-7f:
Observed
In
figures 4-7d and e, a UG modeled galaxy is demonstrated to bear a
resemblance to the general morphology
and properties of the Andromeda
galaxy. Note that the
rotating distorted hourglass structure at the center of the
calculated galaxy (figure 4-7e) bears a resemblance to the general
structure of Andromeda’s nucleus
(figure 4-7f), additionally accounting for the two short spirals
observed to extend from the nucleus and for the ansae
reported by Beaton et al. in 2005 (Beaton
et al., 2005).

Figure
4-12a: Depicts an
image of the effect of a companion galaxy on a modeled galaxy,
compared with the observed cartwheel galaxy ESO
350-40 (figure 4-12b).
Note that both galaxies
demonstrate clumps of star formation.
Figure
4-12b: The Cartwheel
Galaxy, ESO 350-40.
Image credit: NASA,
ESA, and K. Borne (STScI),
http://hubblesite.org/gallery/album/pr2007017d.
In Chapter V, the UG theory is applied to model the general structure
of Saturn’s main body of rings. Saturn’s ring system was
first observed by Galileo nearly 400 years ago, 77 years prior to
Newton’s discovery of the gravitational force. Despite the
extensive study of planetary rings, the origin and many of the
properties of Saturn’s complex ring system remain a mystery.
Figure 5-1 provides a comparison between a UG calculated model and a
computer-generated image of Saturn’s ring system using RSS
3-wavelength occultation data.


A detailed, high
resolution image of Saturn’s D ring is displayed in Figure 5-2.
Figure 5-7a displays a detail of Saturn’s A ring interior to
the Encke Gap taken by the Cassini ISS instrument. On the right the
image reveals spiral bending waves, where the wavelength decreases
inwards, and on the left a succession of spiral density waves, where
the wavelength decreases outwards. The same structure is revealed in
the calculated image 5-7c.

Figure
5-2a:Saturn’s D ring,
NASA/JPL/Space Science
Institute,
http://photojournal.jpl.nasa.gov/catalog/?IDNumber=PIA08990.
Figure
5-2c:A comparison between a calculated image of Saturn’s
D ring
(figure 5-2c) and the observed D ring (figure 5-2a).

Figure
5-7a: Saturn’s
A ring interior to the
Encke Gap. Image
credit:
NASA/JPL/Space Science
Institute; http://photojournal.jpl.nasa.gov/catalogue/PIA06093.
Building on the same equations, the UG theory
will be applied in Chapter VI to explain galactic dynamics. The
unified gravitational equations will be shown to provide for
the constant velocity curve observed in spiral galaxies, as well as
for high stellar velocities, without relying on the auxiliary
hypothesis of dark matter. The chapter will additionally discuss the
origin of galactic wind and the
mechanism underlying star formation and fragmentation.
Chapter VII will discuss the implications of unified gravitation on
general relativity and on the current cosmological model. In
addition, the formation of galactic voids, the triggering mechanism
and the driving forces behind the massive outflow of gas and matter
observed during novae or supernovae, the clustering of nearby
galaxies, and the effective repulsion between distant galaxies will
be addressed. Finally, the theory of unified gravitation will be
demonstrated to provide an explanation for the observed expansion of
the universe while avoiding the dilemmas that led to the adaptation
of inflation theory and to the assumptions of dark matter and dark
energy, thus providing a significantly simpler model.
Additional applications of the UG equation will be discussed in the
following chapters. Chapter VIII is concerned with the processes of
ionization and their sources of energy. Chapter IX will discuss the
structure and composition of planets and the mechanisms that
determine whether a given planet will develop into a terrestrial or
gas planet, and whether or not a given planet will demonstrate a ring
system. The chapter will additionally propose a possible explanation
for the generation of planetary magnetic fields. In Chapter X the
question of galactic redshift periodicity will be contemplated.
As the fundamental premise of the UG theory is the unification of
gravitation and the strong interaction, the final chapter will
demonstrate the applicability of the unified gravitational equations
on nuclear scales, where the UG theory will be demonstrated to
account for the observed weak fall-off of the deep inelastic
scattering cross section, and to provide a scaling behavior similar
to Bjorken scaling.
|



